Positional Encoding 종류 / 2D Sinusoidal Encoding, Rotary Positional Embedding (RoPE) 개념, inductive bias란 - ViT

Transformer 구조(원래 NLP 분야에서 제안됨)는 현재 Computer Vision 영역에서도 SOTA 성능을 보이고 있다. 그러나 Vision Transformer(ViT)는 CNN과 달리 local processing이나 translation invariance와 같은 spatial inductive bias가 내장되어 있지 않다. 비전 영역에서 ViT는 이미지를 patch 단위로 분해하여 sequence로 처리하는데, 이 과정에서 원래의 2D 구조 정보가 사라진다. 따라서 Positional Encoding(PE)은 ViT가 이미지의 공간 정보를 학습하도록 만드는 핵심 요소이다.

Positional Encoding의 중요성

Self-attention은 순서를 고려하지 않는(permutation-invariant) 구조이다. 즉, 입력 token 순서를 바꿔도 내부 동작은 동일하다. 그러나 vision과 language에서는 absolute + relative 위치 정보가 의미를 결정한다. PE는 각 token에 위치 정보를 추가함으로써 attention이 위치적 의미를 구분할 수 있도록 symmetry를 깨는 역할을 한다.

Vision Transformer의 취약점

이미지를 patch로 나누면, geometry 정보가 사라진다. PE가 없다면 ViT는 이미지 전체를 bag-of-patches로 처리하게 되며, 예를 들어 “이 texture가 왼쪽 상단의 하늘인지, 오른쪽 하단의 땅인지”를 구분할 수 없다. 이 때문에 학습 수렴과 일반화가 모두 저하된다.

 

 

 

(1) 2D Sinusoidal Encoding

• row/column에 대해 독립적으로 sin/cos 주파수를 부여
• absolute position encoding
• deterministic, learnable parameter 없음

(2) Rotary Positional Embedding (RoPE)

• Query/Key 벡터에 rotation을 적용하여 **relative distance(m−n)**가 attention score에 직접 반영됨
• relative positional inductive bias를 제공

 

• Sinusoidal: 가장 강한 grid prior, low-resolution 데이터에서 generalization 최고
• RoPE: relative bias + 높은 capacity, 그러나 generalization gap 존재

 

 

---

 

---

Vision Transformer에서 Positional Encoding과 Inductive Bias 정리

— Sinusoidal Encoding과 RoPE 중심

Vision Transformer(ViT)는 이미지 분류, detection, generation 등 여러 비전 과제에서 뛰어난 성능을 보이는 모델 구조임. 하지만 ViT는 이미지의 2D 공간 구조(spatial structure)에 대한 선천적인 감각이 거의 없는 모델이라는 중요한 한계를 가짐.
반대로 CNN은 구조 자체에 locality와 translation equivariance 같은 성질이 들어 있어, 이미지를 다룰 때 유리한 inductive bias를 자연스럽게 가진다.

• Inductive bias가 무엇인지
• 왜 ViT에서 **Positional Encoding(PE)**이 필수인지
• 2D Sinusoidal PE와 **RoPE(Rotary Positional Embedding)**가 각각 어떤 inductive bias를 주는지

 

---

1. Inductive Bias란 무엇인가?

1.1 직관적인 정의

머신러닝 모델은 항상 보지 않은 데이터에 대해 예측을 해야 함.
그런데 우리가 가진 데이터는 유한하고, 실제 세계의 경우의 수는 거의 무한에 가까움.
이때 “어떤 규칙이 더 그럴듯한가?”를 정하는 기준이 필요하며, 이것이 바로 inductive bias임.

조금 더 형식적으로 말하면,

Inductive bias란, 모델이 제한된 데이터로 학습한 뒤
관측하지 않은 새로운 입력에 대해 어떤 형태의 함수/패턴을 더 선호하여 일반화할 것인가에 대한 암묵적인 가정들의 집합이라고 할 수 있음.

1.2 예시로 보는 inductive bias

• Linear Regression
  • “정답은 입력 feature의 선형 결합으로 표현될 수 있음”이라는 가정
  • → 직선/평면 형태의 함수들을 더 선호함
• k-NN
  • “서로 가까운 점들은 비슷한 label을 가질 것”이라는 가정
  • → 유클리드 거리 기반의 local smoothness를 bias로 가짐
• CNN
  • 작은 커널로 local neighborhood만 보는 구조
  • 동일한 필터를 위치에 상관없이 공유(weight sharing)
  • → “근처 픽셀끼리는 강하게 연관됨”, “같은 패턴은 위치가 바뀌어도 같은 의미를 가짐”이라는 강한 공간적 inductive bias를 내장함
• Transformer (PE 없음)
  • 입력 token을 순서 없는 집합처럼 처리할 수 있는 구조
  • → “token 간의 순서나 위치에 대한 선천적 가정이 거의 없음”

1.3 ViT의 문제: Spatial Inductive Bias의 부재

Vision Transformer는 이미지를 patch로 나누고, 이를 flatten된 token의 시퀀스로 처리함.
이때, 모델 구조만 보면:

• 어디가 위인지, 아래인지
• 어떤 patch가 서로 이웃인지
• 두 patch의 거리가 멀리 떨어졌는지

와 같은 정보를 스스로는 전혀 알 수 없음.
즉, ViT는 CNN에 비해 spatial structure에 대한 inductive bias가 거의 0에 가까운 상태에서 시작함.

그래서 ViT는 Positional Encoding을 통해 “위치에 대한 감각”을 외부에서 주입받아야 함.

---

2. 왜 Positional Encoding이 필요한가?

2.1 Self-Attention의 permutation invariance

Transformer의 핵심 연산인 self-attention은 다음과 같이 정의됨:

\[
Q = X W_Q,\quad K = X W_K,\quad V = X W_V
\]

\[
\text{Attention}(Q, K, V) = \text{softmax}\left( \frac{QK^\top}{\sqrt{d_k}} \right) V
\]

여기서 (X)는 입력 token들의 집합이며, 각 행이 하나의 token embedding임.

중요한 점은:

• 입력 토큰의 순서를 섞어도 (예: ([x_1, x_2, x_3]) → ([x_3, x_1, x_2]))
• self-attention은 순열(permutation)에 대해 구조적으로 같은 형태로 동작한다는 것임.

즉, self-attention만으로는

“이 token이 전체 시퀀스에서 몇 번째인지,
혹은 이미지에서 어느 위치에서 온 token인지”

를 알 수 없음.

2.2 Positional Encoding의 역할

따라서 ViT는 patch embedding에 위치 정보를 반영한 벡터를 더하거나(혹은 결합하여) 입력으로 사용함.
일반적인 구조는 다음과 같음:

\[
X_{\text{input}} = X_{\text{patch}} + P_{\text{pos}}
]\

• (X_{\text{patch}}): patch에서 온 내용(content) 임베딩
• (P_{\text{pos}}): 해당 patch의 위치(position)를 나타내는 임베딩
• (X_{\text{input}}): self-attention에 들어가는 최종 입력

이렇게 하면 attention은 내용과 더불어 위치까지 함께 고려하면서 상호작용을 하게 되며,
결과적으로 ViT에 positional inductive bias가 주입됨.

---

3. 2D Sinusoidal Positional Encoding (Absolute)

 

3.1 1D Sinusoidal의 기본 아이디어

 

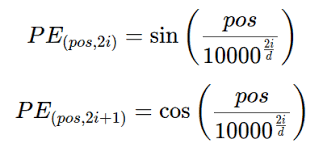
원래 Transformer 논문(Vaswani et al.)에서 제안된 1D Sinusoidal PE는,
시퀀스 내 위치 (pos)와 채널 인덱스 (i)에 대해 다음과 같이 정의됨:

\[
PE(pos, 2i) = \sin\left( \frac{pos}{10000^{2i/d}} \right)
\]
\[
PE(pos, 2i+1) = \cos\left( \frac{pos}{10000^{2i/d}} \right)
\]

여기서:

• (d)는 embedding dimension
• (2i)／(2i+1)은 짝수/홀수 채널을 각각 sin/cos에 대응시킨 것임
• 분모의 (10000^{2i/d}) 항으로 인해, 채널마다 다른 주파수를 가지는 sin/cos 파형을 생성함

결과적으로:

• 낮은 주파수 채널은 장거리 위치 차이를 반영
• 높은 주파수 채널은 근거리 위치 차이를 더 세밀하게 반영

이렇게 함으로써, 각각의 위치 (pos)는 (d)-차원 공간에서 유일한 주기적 패턴을 갖게 되고,
모델은 이 패턴을 통해 “이 token이 시퀀스 내 어디에 있는지”를 구분할 수 있게 됨.

3.2 2D로 확장: 이미지에서의 Sinusoidal PE

이미지에서는 위치가 단일 스칼라가 아니라, ((x, y)) 좌표를 가짐.
따라서 보통 다음과 같이 구현함:

1. **row 방향((x))**에 대해 1D sinusoidal PE를 생성
2. **column 방향((y))**에 대해 1D sinusoidal PE를 별도로 생성
3. 두 벡터를 concat하거나 더해서 최종 2D positional vector를 구성

예를 들어,
이미지 크기가 (H \times W)이고, 각 patch가 1개의 grid cell에 대응된다고 할 때,

• row index (r \in {0, \dots, H-1})
• col index (c \in {0, \dots, W-1})

일 때,

\[
PE^{(x)}(r, 2i) = \sin\left( \frac{r}{10000^{2i/d_x}} \right),\quad
PE^{(x)}(r, 2i+1) = \cos\left( \frac{r}{10000^{2i/d_x}} \right)
\]

\[
PE^{(y)}(c, 2j) = \sin\left( \frac{c}{10000^{2j/d_y}} \right),\quad
PE^{(y)}(c, 2j+1) = \cos\left( \frac{c}{10000^{2j/d_y}} \right)
\]

그 후,

• (;PE(r,c) = [PE^{(x)}(r),,PE^{(y)}(c)])
  혹은
• (;PE(r,c) = PE^{(x)}(r) + PE^{(y)}(c))

처럼 결합하여 최종 positional vector를 구성함.

3.3 Sinusoidal PE가 주는 inductive bias

Sinusoidal PE는 다음과 같은 특징을 가짐:

1. Absolute position 기준
   • 각 grid cell의 절대 위치 ((r, c))에 대해 고유한 벡터를 부여함
   • 모델은 “이 patch가 이미지의 어느 위치에 존재하는지”를 절대 좌표 관점에서 구분할 수 있음
2. 특정 수학적 구조 유지
   • 인코딩이 deterministic하며 학습 파라미터가 없음
   • 다양한 scale의 위치 차이를 sin/cos 주파수로 표현
   • extrapolation(더 긴 시퀀스 등)에 어느 정도 robustness를 가짐
3. Grid topology에 대한 강한 prior
   • 이미지가 고정된 격자 구조 위에 있다고 가정함
   • 특히 CIFAR-10 같이 해상도가 낮고 구조가 단순한 데이터에서는,
     이 grid 기반 절대 위치 bias가 generalization에 도움을 줄 가능성이 큼

요약하면, 2D Sinusoidal PE는:

“이미지는 규칙적인 2D 격자 위에 놓여 있으며,
각 위치는 절대적인 좌표 ID를 가진다”

라는 inductive bias를 ViT에 부여함.

---

4. RoPE (Rotary Positional Embedding): Relative Position Encoding

이제 RoPE를 살펴봄. RoPE는 “**회전(rotation)**을 이용해 positional 정보를 Query/Key에 직접 주입하는 방법”임.

 

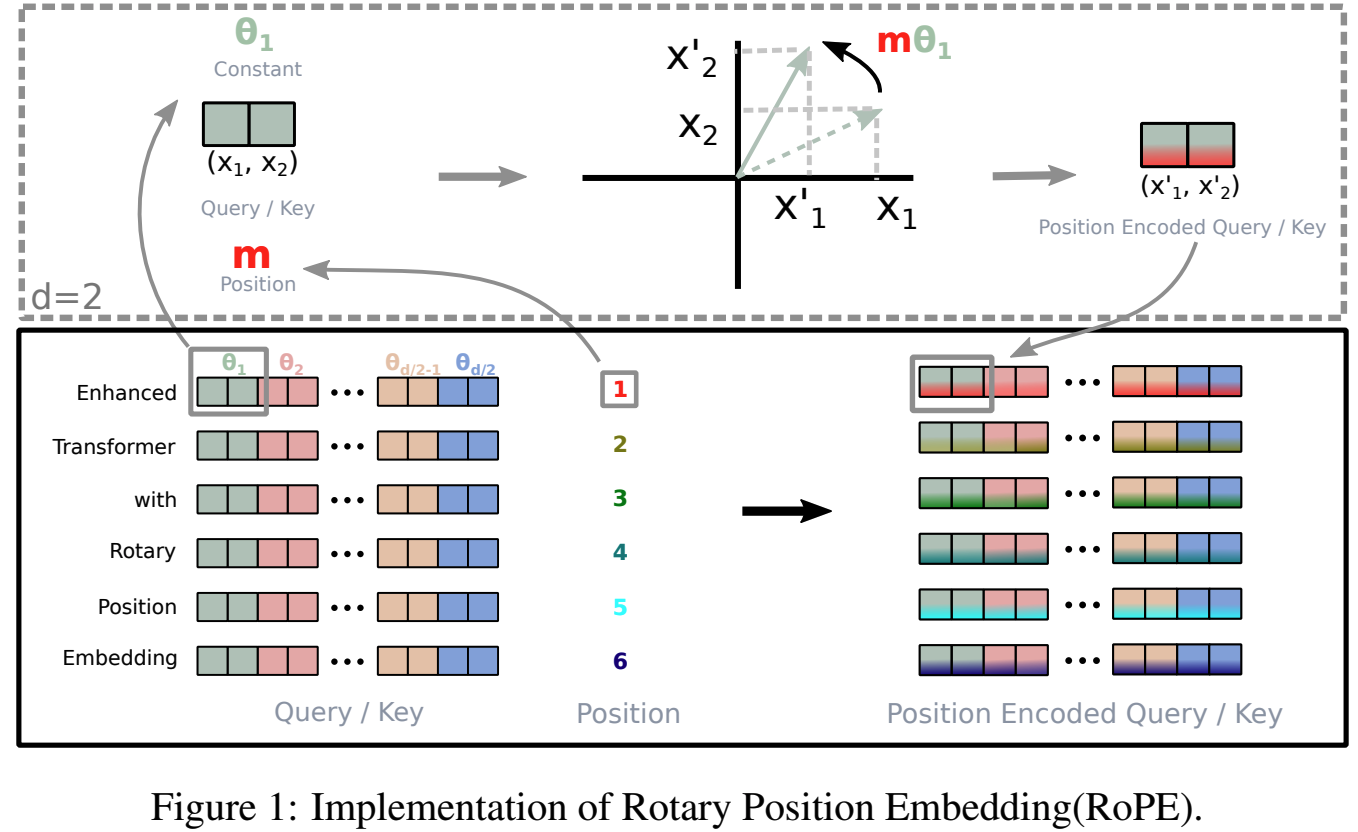
4.1 기본 아이디어: 회전 행렬

2차원 벡터 (\mathbf{x} = (x_1, x_2)^\top)에 대해,
각도 (\theta)만큼 회전하는 연산은 다음과 같은 행렬 곱으로 표현됨:

\[
R(\theta) =
\begin{pmatrix}
\cos\theta & -\sin\theta \
\sin\theta & \cos\theta
\end{pmatrix}
\]

\[
R(\theta)
\begin{pmatrix}
x_1 \
x_2
\end{pmatrix}

\begin{pmatrix}
x_1\cos\theta - x_2\sin\theta \
x_1\sin\theta + x_2\cos\theta
\end{pmatrix}
\]

고차원 벡터에 대해서는, 차원을 2개씩 묶어
((x_1,x_2), (x_3,x_4), \dots)에 각각 다른 각도의 회전을 적용하는 식으로 확장함.

4.2 RoPE에서의 위치에 따른 회전

 

RoPE는 token의 위치 index를 회전 각도에 반영함.

• 위치 (m)에 있는 query 벡터를 (\mathbf{q}_m)
• 위치 (n)에 있는 key 벡터를 (\mathbf{k}_n)라 할 때,

RoPE는 다음과 같이 변환된 벡터를 사용함:

\[
\tilde{\mathbf{q}}_m = R(m\theta),\mathbf{q}_m,\quad
\tilde{\mathbf{k}}_n = R(n\theta),\mathbf{k}_n
\]

여기서 (\theta)는 실제로는 고차원에서 채널마다 다른 주파수를 가지도록 일반화되지만,
핵심 개념 이해를 위해 단일 각도로 표기함.

4.3 상대 위치만 남는 내적의 성질

RoPE의 가장 중요한 수학적 성질은 다음과 같음.

회전 행렬 (R(\theta))는 orthogonal이므로 다음을 만족함:

\[
R(\theta)^\top R(\theta) = I
\]

이제 RoPE 적용 후 query와 key의 내적(dot product)을 계산해봄:

\[
\langle \tilde{\mathbf{q}}_m, \tilde{\mathbf{k}}_n \rangle
= \langle R(m\theta)\mathbf{q}_m, R(n\theta)\mathbf{k}_n \rangle
\]

내적의 성질과 회전 행렬의 orthogonality를 이용하면:

\[
\langle R(m\theta)\mathbf{q}_m, R(n\theta)\mathbf{k}_n \rangle
= \langle \mathbf{q}_m, R(m\theta)^\top R(n\theta)\mathbf{k}_n \rangle
\]

\[
R(m\theta)^\top R(n\theta)
= R(-m\theta) R(n\theta)
= R((n-m)\theta)
\]

따라서,

\[
\langle \tilde{\mathbf{q}}_m, \tilde{\mathbf{k}}_n \rangle
= \langle \mathbf{q}_m, R((n-m)\theta)\mathbf{k}_n \rangle
\]

즉, attention score(내적)가 (m)과 (n)의 절대 위치가 아니라,
오직 상대 거리 ((n-m))에 의존하는 구조가 됨.

이것이 RoPE가 가지는 핵심적인 상대적 positional encoding 성질임.

4.4 RoPE가 주는 inductive bias

위 수식으로부터 RoPE가 제공하는 inductive bias는 다음과 같이 정리할 수 있음.

1. Relative position 중심
   • self-attention이 두 token 사이의 절대 위치보다,
     두 위치 간의 **차이(거리)**를 더 직접적으로 반영함
   • 예: “왼쪽에서 2칸 떨어진 패치” 같은 상대적 관계
2. Rotation을 통한 position mixing
   • 위치에 따른 회전을 통해,
     query와 key의 표현공간에서 위치 정보가 자연스럽게 섞이도록 함
   • 이는 순수 add 방식(단순 (X+P))보다 풍부한 표현력을 가질 수 있음
3. Translation에 대한 robustness
   • 상관관계가 상대 거리 ((n-m))로 표현되므로,
     전체 시퀀스가 한 칸씩 shift되는 상황에서
     동일한 상대 관계를 유지하는 경향을 가지게 됨

결론적으로 RoPE는,

“패치 간의 상대적 거리와 방향이 중요하며,
절대 위치 자체보다 상대적 geometry를 더 중시한다”

는 형태의 positional inductive bias를 ViT에 부여함.

---

5. Sinusoidal vs RoPE: 어떤 상황에서 무엇이 유리한가?

두 방식 모두 ViT에 필수적인 positional 정보를 주입하지만, 그 관점이 다름.

방식 위치 정보 유형 주요 inductive bias 장점 잠재적 단점

Sinusoidal (2D)	Absolute	고정 grid 위의 절대 좌표	구조 단순, 안정적, low-res에서 강함	상대적 관계 표현이 직접적이지 않음
RoPE	Relative	위치 간 간격과 방향	상대적 geometry 표현에 강함, 표현력↑	세팅에 따라 generalization gap 가능

• CIFAR-10 같이 해상도가 낮고 grid 구조가 명확한 데이터에서는
  명시적인 격자 구조를 encode하는 Sinusoidal PE가 generalization에서 더 유리할 수 있음.
• 반대로, 복잡한 장면, 긴 시퀀스, 상대 위치 관계가 중요한 설정에서는
  RoPE의 relative positional encoding이 더 큰 이점을 줄 수 있음.

---

6. 정리

• Vision Transformer는 구조적으로 spatial inductive bias가 거의 없는 모델이며,
  Positional Encoding은 이 한계를 보완하는 핵심 요소임.
• 2D Sinusoidal PE는
  “이미지는 고정된 2D grid 위에 있으며, 각 위치는 절대 좌표 ID를 갖는다”는
  강한 grid 기반 inductive bias를 제공함.
• RoPE는
  Query/Key에 위치 기반 회전을 적용하여,
  self-attention score가 위치 간 상대 거리에 의해 결정되도록 만들며,
  “상대적인 geometry와 관계”를 더 중시하는 inductive bias를 제공함.
• 어떤 방식이 더 좋은지는
  • 데이터의 해상도,물체의 배치 특성,augmentation 전략,과제가 요구하는 invariance의 성질 등에 따라 달라짐.

결국 Positional Encoding

ViT가 세상을 어떤 구조로 이해하도록 만들 것인가를 설계하는 장치,
즉 ViT의 positional inductive bias를 디자인하는 방법이라고 보는 것이 타당함.

---

RoPE에서 “각도로 회전한다”라는 표현이 처음 보면 헷갈리는 게 정말 정상임.
많은 사람들이 처음에 “이미지를 회전시키는 건가?”라고 오해함.
하지만 RoPE는 이미지나 patch를 회전시키는 게 아니라, 벡터 값을 회전시키는 것임.

 

RoPE가 회전시키는 대상은 이미지나 patch가 아니라, patch embedding 벡터의 좌표, 즉 숫자 공간(vector space)에서의 방향임.

---

비유 이해

• 사람 얼굴 사진이 있다고 하자
  RoPE가 하는 일은 사진을 돌리는 게 아니라,
  사진을 설명하고 있는 벡터(숫자 리스트)의 방향을 조금 회전시키는 것임.

즉, 영상 데이터를 돌리는 게 아니라, 해당 위치의 token embedding 벡터를 수학적으로 회전시키는 것임.

---

좀 더 구체적으로

비유:
어떤 patch를 표현하는 벡터가 있다고 하자.

예를 들어, patch embedding이
\[
(0.5,, 0.1)
\]
이라고 하면, 2D 좌표 평면에서 점 1개라고 생각할 수 있음.

RoPE는 “이 patch가 이미지 내에서 몇 번째 위치에 있는지”에 따라
이 벡터에 **회전 변환(rotation matrix)**을 곱함.

예를 들어, 다음과 같이 변할 수 있음:

\[
(0.5,, 0.1) \rightarrow (0.468,, 0.241)
\]

겉으로 보면 단순히 벡터 숫자들이 바뀐 것이지만,수학적으로는 “벡터가 특정 각도만큼 회전되었다”고 표현함.

---

왜 굳이 벡터를 회전시키는가?

벡터를 회전시키면 좋은 점이 있음:

• query 벡터의 회전 정도 – key 벡터의 회전 정도
  → 두 token 간의 위치 차이(상대 거리)를 자연스럽게 반영

예:

상황 두 벡터의 상대적 회전 차이

서로 가까운 위치	회전 차이가 작음 → dot product↑ (attention↑)
서로 멀리 떨어진 위치	회전 차이가 큼 → dot product↓ (attention↓)

즉, 회전 양을 다르게 줌으로써 상대적인 위치 차이를 attention score에 반영하는 방식임.

그래서 “이미지를 회전”하는 게 아니라:

• patch embedding 벡터의 방향을 수학적으로 회전
• 그 회전량으로 위치 정보를 표현
  이게 RoPE의 핵심.

 

• RoPE → “이 patch는 이 위치에 있으니까, 벡터의 방향을 위치만큼 틀어줄게”
• 그러면 다른 위치 벡터와의 방향 차이로 상대거리까지 자연스럽게 드러남

생각해봐:

• 같은 방향을 가리키는 두 벡터는 비슷한 의미
• 멀리 다른 방향을 가리키면 다른 의미

RoPE는 이 벡터 방향 차이로 패치들 사이의 거리와 상대 관계를 attention에 전달하는 구조임.

RoPE는 이미지를 회전시키는 게 아니라,
위치 인덱스에 따라 embedding 벡터를 수학적으로 회전시키고,
벡터들 사이의 회전 차이로 상대적 위치 관계를 attention에 반영하는 기법임.

---