
diffusion model
Diffusion model은 “정보를 점점 noise로 덮었다가, 그걸 다시 복원하면서 이미지(또는 데이터)를 생성하는 모델”
• forward 과정: 깨끗한 이미지를 noise로 점점 망가뜨림
• reverse 과정: noise를 조금씩 제거해서 원래 이미지를 복원함 → 여기서 이미지를 새로 생성할 수도 있음!
🧠 핵심 개념: Score-based Diffusion
• score function: “지금 이 데이터가 어디로 가야 더 깨끗해질까?”를 알려주는 방향 정보
• 그 방향 정보를 따라가면 → 노이즈 제거 → 이미지 생성!
🔹 수식 (1)

dx = f(t)xdt + g(t)dw
• forward diffusion 과정을 수학적으로 표현.
• x: 현재 시점의 latent 상태 (노이즈가 섞여 있음)
• f(t): 시간에 따라 변하는 데이터의 drift (데이터가 어디로 흐를지)
• g(t): 얼마나 노이즈를 섞을지
• dw: 랜덤한 noise (Brownian motion, 즉 랜덤으로 움직임)
점점 더 이미지를 노이즈로 바꿔가는 과정.
즉, 깨끗한 이미지 → 점점 노이즈 이미지로 바뀜.
🔍 w: Wiener process (브라운 운동)
• w는 수학적으로 Brownian motion 또는 Wiener process를 뜻함.
• 시간에 따라 완전 랜덤 하게 움직이는 함수.
• dw는 그 미분형태로, 아주 짧은 시간에 일어나는 무작위 변화량.
Q1. 수식 (1)에서 왜 좌변이 dx인가?
“왜 현재 시점의 latent 상태를 미분해야 하지? dx가 중요한 이유는?”
수식 (1)은 일반적인 **확률 미분 방정식 (SDE: Stochastic Differential Equation)**의 형식. 이 식에서 dx는 “**time t**이 아주 조금 변했을 때, latent 상태 x가 얼마나 변하는가”를 의미함.
• dx: 작은 시간 변화 dt 동안, x가 얼마나 변화하는지
• 즉, 이건 “변화량의 모델링”. deterministic (규칙적) + stochastic (랜덤) 변화의 합으로 모델링하는 것.
🎯 왜 중요하냐면?
• diffusion model은 시간에 따라 데이터가 어떻게 노이즈로 바뀌는가를 모델링함.
• 그 변화 과정을 제대로 추적하려면 미분 기반 표현이 필요함.
• 특히, SDE에서는 “데이터가 어떻게 랜덤하게 움직이는지”를 기술할 수 있는 유일한 도구가 바로 이런 미분 표현임.
🔹 수식 (2)

dx = \left[f(t)x - \frac{1}{2}g^2(x)\nabla_x \log(q_t(x))\right]dt
• reverse diffusion, 즉 노이즈를 제거하면서 원래 이미지로 돌아가는 과정
• \nabla_x \log(q_t(x)): 현재 데이터 분포의 score function임.
→ 지금 x가 어디로 가야 진짜 이미지 분포에 가까워지는지를 알려줌.
• 이건 데이터가 어디로 가야 “덜 노이즈스럽게” 될지를 알려주는 방향 vector
결론: 이 식은 노이즈 제거 방향으로 천천히 이동하는 수학적 표현.
Q2. w, dw는 뭐고 왜 t로 바뀌었지?
왜 수식 (2)에서는 dw가 사라지고 dt만 남았을까?
• 수식 (1)은 forward diffusion, 즉 데이터에 노이즈를 추가하는 과정
• 수식 (2)는 reverse diffusion, 즉 노이즈를 제거하는 과정인데
• 이 reverse 과정은 확률적이 아니라 평균적인 경로(ODE)로 기술됨!
그래서,
• 수식 (2)는 확률적 SDE를 평균적인 역방향 경로로 바꾼 deterministic ODE
• 여기서는 노이즈가 아닌 score function 방향으로만 이동하므로 dw가 사라짐.
수식 (2)는 기본적으로 SDE의 역과정(Schrödinger bridge 해석)을 deterministic하게 기술한 것임.
Q3. dt는 왜 t에 대해 미분하는 거지? 모든 게 t 기준?
그렇다. diffusion model은 시간 t를 축으로 두고 전개됨.
• 시간 t = 0이면 깨끗한 이미지
• 시간 t = 1이면 완전한 노이즈
• diffusion은 이 시간 흐름에 따라 이미지를 노이즈화하거나 반대로 노이즈를 제거함
따라서 모든 변화량은 시간 기준의 미분량으로 표현 :
dx = \text{데이터가 시간 } t \text{동안 어떻게 움직이는가}
Q5. 수식 (1) → 수식 (2)에서 왜 g(t)가 -\frac{1}{2}g^2(x)로 바뀌어?
Ito calculus (확률 미적분) 를 기반으로 한 변화.
• 수식 (1)은 SDE, 수식 (2)는 역방향 ODE
• 이때 SDE에서 ODE로 바꾸는 과정에서, score function 항이 gradient와 결합되면서 -\frac{1}{2}g^2(x)\nabla_x \log q_t(x) 형태가 나옴.
이건 확률 해석학적으로 증명된 결과이고, noise 항이 역방향 score에 어떤 영향을 주는지를 수학적으로 반영.
🔹 수식 (3)

\mathcal{L} = \gamma(t)\|S_\theta(x, t) - \nabla_x \log(q_t(x))\|^2_2
• score function을 학습하는 loss 함수
• S_\theta(x, t): 모델이 학습해서 만든 score function (예: U-Net이 출력하는 결과)
• 오른쪽의 true score와 얼마나 가까운지를 계산해서 학습함.
쉽게 말해, “진짜 방향”이랑 “내가 예측한 방향”의 차이를 줄이려고 학습
Q4. 수식 (3)의 \gamma(t)는 왜 곱하지?
\mathcal{L}은 loss function, 학습 시 사용하는 손실 함수
• 여기서 \nabla_x \log q_t(x): 진짜 score (데이터 분포의 gradient)
• S_\theta(x, t): 학습된 모델의 출력 (예: U-Net의 출력)
• \gamma(t): 시간에 따라 각 샘플의 loss 중요도를 조절하는 가중치 함수
왜 필요하냐면?
• 초기에 노이즈가 많을수록, score 추정이 더 불확실하고 중요한 역할을 함.
• 그래서 시간 t에 따라 loss를 다르게 줄 필요가 있음 → 이걸 조절하는 게 \gamma(t)
🔹 수식 (4)
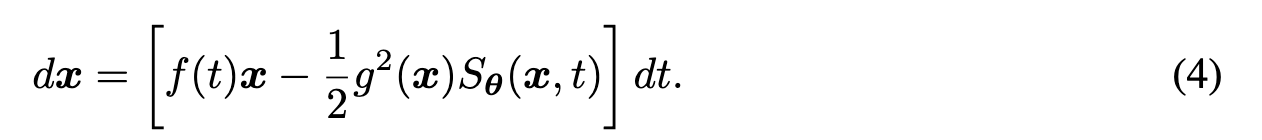
dx = \left[f(t)x - \frac{1}{2}g^2(x)S_\theta(x, t)\right]dt
👉 위의 수식 (2)에서 모델이 학습한 score function S_\theta을 집어넣은 버전
이 수식으로 노이즈 제거 과정을 진행하면서 깨끗한 이미지를 복원함.
🔹 수식 (5)

dx = \left[f(t)x - \frac{1}{2}g^2(x)\frac{\mu_t - x}{\sigma^2(t)}\right]dt
좀 더 실제 구현에 가까운 식
• \mu_t: 현재 노이즈 이미지 x에서 denoising한 결과 (깨끗한 이미지 추정)
• \sigma(t): 현재 시점의 noise 수준
“지금 noisy image x와 깨끗한 예측값 \mu_t” 사이의 차이를 보고, 그 방향으로 얼마나 이동할지를 계산한 것.
Q6. 수식 (4) → (5)에서 왜 \sigma(t)^2로 나눠? 가우시안이랑 관련 ?
배경:
• 대부분의 diffusion model은 Gaussian noise를 사용함.
• 이 때 score function은 다음과 같은 형태로 근사:
\(\nabla_x \log q_t(x) \approx \frac{\mu_t - x}{\sigma^2(t)}\)
→ 이건 denoising score matching에서의 closed-form score임. 즉, 정답 이미지 \mu_t와 현재 noisy 샘플 x의 차이로 score를 계산하는 방식.
그래서 수식 (5)는 학습된 score를 직접 쓰는 대신, Gaussian 가정 하에서 계산된 score를 사용하는 형태로 바뀜.
🔹 수식 (6)

dx = \frac{x - \mu_t}{\sigma(t)} d\sigma(t)
👉 특수한 경우: variance exploding (VE) diffusion.
• 식 (5)의 특별한 조건에서 단순화된 것임
• x에서 \mu_t 방향으로 noise를 줄이면서 이동함.
이건 실제 구현에서 자주 쓰이는 형태로, 노이즈 제거 경로를 따라 이동하는 단순한 표현
1. sigma란?
정확한 의미:
sigma는 noise scale, 즉 diffusion process에서 각 시간 단계(timestep)에 해당하는 노이즈의 세기입니다.
• diffusion 모델은 이미지를 점점 noise로 바꾸는 forward process와
• 노이즈에서 이미지를 복원하는 reverse process (denoising) 를 반복합니다.
• 이때 각 단계마다 얼마나 noisy한 샘플을 처리해야 하는지 정해주는 값이 바로 sigma.
Stable Diffusion에서의 역할:
• sigma는 denoising loop에서 사용되며, noise level이 높은 초기 단계부터, 점점 noise가 줄어드는 후반 단계까지 스케줄링되어 있습니다.
• scheduler.set_timesteps()를 통해 noise level (sigma) 리스트가 설정됩니다.
• 즉, sigma_list는 timestep에 대응되는 노이즈 강도의 리스트라고 보면 됩니다.
예시:
sigma_list = np.load('sigmas/sigmas_25.npy')
• 이건 inference 단계에서 사용할 noise schedule로,
• 25개의 timestep에 해당하는 noise level을 의미합니다.
(예: timestep 0에는 sigma=5.0, timestep 1에는 sigma=4.3 … 이런 식)
2. num_frames은 뭐고 왜 맞춰야 해?
num_frames의 의미:
• 생성할 비디오의 프레임 수입니다.
• 예를 들어 num_frames = 10이면 10장의 이미지 (시점별 view) 를 생성합니다.
• 이건 곧 하나의 카메라 트랙을 따라간 결과물이죠.
왜 num_frames과 sigma_list는 연관이 있는가?
lambda_ts (lambda schedule)는 (sigma 개수) × (num_frames 개수) 만큼의 weight를 계산합니다:
lambda_t_list_optimized = lambda_t_list_optimized.reshape([len(sigmas), num_frames])
즉, search_hypers() 함수에서:
• 각 sigma에 대해,
• 각 프레임별로 lambda_t라는 가중치를 계산합니다.
그래서 len(sigmas) * num_frames 개수만큼의 값이 필요합니다.
👉 하나라도 길이가 안 맞으면 reshape 에러 발생!
💡 요약 정리
항목 의미 예시
| sigma | timestep에 해당하는 noise level (scheduler에서 사용) | [5.0, 4.3, …, 0.1] (25개) |
| num_frames | 생성할 영상의 프레임 수 | 10이면 영상은 10장짜리 |
| 둘의 연관 | lambda_ts 계산 시 sigma × num_frames만큼 weight 생성 | [25, 10]이면 250개 필요 |
왜 lambda_ts가 (sigma 개수 × num_frames)만큼 필요한가?
모델이 “각 timestep(sigma)에 대해 모든 frame에 다르게 반응하도록” 설계되어 있기 때문이에요.
기본 아이디어
이 구조는 2D 테이블 형태의 weight 스케줄을 만든다고 생각하시면 돼요.
Frame 0 Frame 1 ... Frame N
sigma_0 λ₀₀ λ₀₁ ... λ₀N
sigma_1 λ₁₀ λ₁₁ ... λ₁N
... ... ... ... ...
sigma_S λS₀ λS₁ ... λSN• sigma_s: s번째 timestep (noise level)
• frame_f: f번째 프레임
• lambda_t[s][f]: s번째 timestep에서 f번째 프레임에 적용할 가중치
왜 이렇게 해야 하느냐?
1. lambda_t는 denoising 반복(loop) 안에서 사용돼요.
• denoising은 timestep마다 진행되므로 sigma 개수 만큼 반복됨
• 매 반복에서, 전체 프레임에 대한 gradient/condition 계산이 들어감
→ 따라서 각 timestep에 대해 모든 프레임의 가중치가 있어야 함
2. 시간(timestep)과 공간(frame)이 모두 중요한 문제
• diffusion이 noise 제거를 timestep 단위로 하듯이,
• 프레임 별로도 temporal variation이 있으므로 frame-wise control도 필요
• 이걸 동시에 조절하려면 (sigma × frame)만큼의 가중치가 필요해요
수식적으로 보면?
lambda_t_list_optimized = lambda_t_list_optimized.reshape([len(sigmas), num_frames])이건 결국 이런 걸 만드는 거예요:
• lambda_t_list_optimized[s][f]
→ s번째 sigma, f번째 frame에 사용할 가중치 λₛf
직관적으로 표현하자면:
• sigma는 시간축
→ “지금 얼마나 noisy한 상태인가?”
• frame은 공간축 (viewpoint)
→ “지금 몇 번째 프레임 (시점)인가?”
• lambda_ts는 이 시간×공간을 커버하는 가중치 테이블
→ noise 강도와 프레임 위치에 따라 다른 보정값을 주는 거죠
결론: 왜 곱하냐?
각 timestep마다 모든 프레임을 커버해야 하니까
→ 전체 weight 수 = timestep 수 (sigma 개수) × 프레임 수 (num_frames)
💡 핵심 용어 정리
1. timestep
• Diffusion process에서 “denoising을 몇 번에 걸쳐 할 것인가”를 결정하는 시간축 개념이야.
• 예: num_inference_steps=25이면, 25개의 timestep을 통해 점점 noise를 제거해 나가며 이미지를 복원해.
• 각 timestep마다 latent는 조금씩 denoise 됨.
2. sigma
• 각 timestep마다 사용되는 noise 수준 (standard deviation) 을 나타내.
• 일반적으로 timestep이 클수록 noise는 크고 (큰 sigma), 작을수록 noise는 적어 (작은 sigma).
• diffusion 모델에서는 시간 t에 대응되는 sigma 값을 사전에 정한 schedule에 따라 사용해.
3. num_frames
• 생성할 비디오 프레임 수. 예: num_frames=25이면 25장의 이미지를 생성하게 돼.
• 각 프레임은 같은 시간축에서 함께 denoising을 당하지만, 위치나 latent 상태는 다를 수 있음.
🧠 구조적으로 어떻게 연관돼 있는가?
✅ 매 timestep마다 일어나는 일:
1. latent tensor는 num_frames개의 프레임에 대해 존재함 (shape: [B, num_frames, C, H, W]).
2. 하나의 timestep에서 전체 프레임(batch of frames) 에 대해 denoising을 수행해.
3. 이 denoising 과정에서, 프레임마다 조금씩 다른 guidance를 줄 수 있도록 하기 위해 frame별 lambda (weight) 를 적용해.
📌 그래서 lambda_ts는 왜 (sigma 개수 × num_frames) 짜리인가?
1. sigma 개수 = inference timestep 수 = num_inference_steps
2. 각 timestep에서 프레임마다 개별로 weight를 주려면, 프레임 수만큼 lambda가 필요해.
3. 따라서 전체 denoising process 동안 총 num_inference_steps × num_frames 개의 weight가 필요하게 돼.
즉, 각 timestep t에 대해 25개의 프레임이 있으면, 그 timestep에서 25개의 lambda를 적용해서 프레임별로 가중치를 다르게 줄 수 있음.
❓ 질문: sigma가 25개면, timestep 하나당 25번 denoise하냐?
➡️ 아니야!
• sigma가 25개라는 건, 총 25개의 timestep이 있고, 각 timestep마다 하나의 sigma가 쓰인다는 뜻이야.
• 각 timestep은 한 번의 denoise만 수행해.
• 대신 그 denoising은 num_frames 개 프레임에 동시에 적용되는 거지.
🧭 비유로 설명하자면…
• 25개의 노이즈 레벨(sigma) = 25개의 정해진 날씨 변화.
• 하루하루(= timestep) 날씨가 달라짐.
• 근데 매 날, 25명의 사람이(= 프레임) 다 같이 외출해야 함.
• 그래서 날마다, 사람마다 옷차림(lambda_ts)을 다르게 챙겨야 하는 거야.