① Blur, ② Periodic Noise, ③ Low Contrast의 세 가지 degradation를 library 없이!!! 직접 구현하는 정석적인 방법
시작 전
나는 Inria Aerial Image Labeling Dataset에서 gt를 골라서 사용하겠다.
https://minsunstudio.tistory.com/102
[Dataset] Inria Aerial Image Labeling Dataset 설명, download 다운로드 하는 법, .tif 파일
Inria Aerial Image Labeling Dataset 이란Link: https://project.inria.fr/aerialimagelabeling/ Inria Aerial Image Labeling DatasetThe dataset The Inria Aerial Image Labeling addresses a core topic in remote sensing: the automatic pixelwise labeling of aeria
minsunstudio.tistory.com
입력: gt = austin1.tif (깨끗한 Ground Truth 이미지) 한장이 필요하다.
출력: degraded.png (세 가지 degradation 모두 적용된 최종 이미지)
① Blur (Gaussian blur 또는 Motion blur)
우리가 알고있는 gaussian distribution 수식은 :
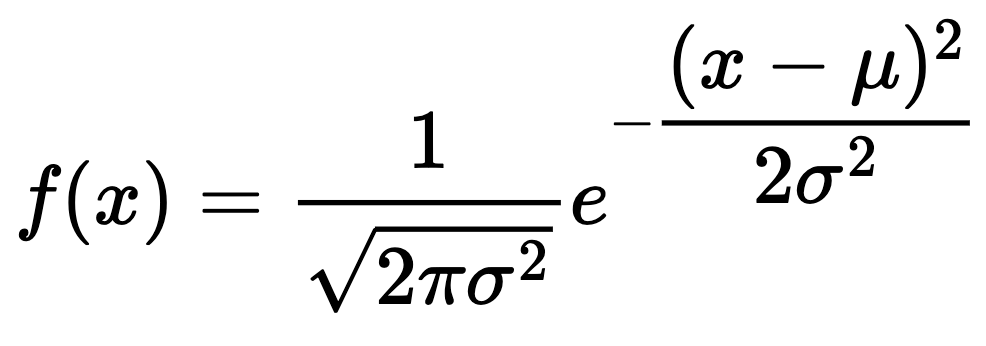
(1) Gaussian blur
원리
가우시안 블러(Gaussian blur)는 주변 픽셀로부터 평균값을 구할 때 가우시안 매트릭스를 사용하여 주변 픽셀에 가중치를 둔다.
이 매트릭스는 연산할 픽셀로부터 가까울수록 높은 가중치를 갖고 멀어질수록 낮은 가중치를 둔다.
(중심에 있는 픽셀에 높은 가중치를 부여한다)
커널(kernel) ( h(x,y) )는 2D Gaussian 함수이다.
\(h(x,y) = \frac{1}{2\pi\sigma^2} e^{-\frac{x^2 + y^2}{2\sigma^2}}\)
컨볼루션을 통해 이미지를 흐리게 만든다.

코드
import numpy as np
import cv2
def make_gaussian_kernel(ksize=9, sigma=2.0):
"""2D Gaussian kernel 생성"""
ax = np.arange(-ksize//2 + 1., ksize//2 + 1.)
xx, yy = np.meshgrid(ax, ax)
kernel = np.exp(-(xx**2 + yy**2) / (2. * sigma**2))
kernel /= np.sum(kernel)
return kernel
def apply_gaussian_blur(img, sigma=2.0):
ksize = int(6*sigma + 1)
kernel = make_gaussian_kernel(ksize, sigma)
blurred = cv2.filter2D(img, -1, kernel)
return np.clip(blurred, 0, 1)
그럼 gaussian filter는?
평균 필터는 대상 점을 주변 픽셀들의 평균값으로 대체하기 때문에 이미지를 블러링(blurring)하는 효과를 가진다.


- 이는 대상 점과 가까운 픽셀이 먼 픽셀보다 더 연관이 있다는 것을 반영하지 않는다.
- 그래서 가우시안 필터를 사용한다.
- 가우스 함수는 대상 점의 값이 가장 크고, 대상 점에서 멀어질수록 값이 작아지는 특징이 있다.
- 가우스 함수의 값 : 표준편차, 얼마나 대상 점에서 멀어지는지 정도 나타냄
- 값이 클 수록 (대상 점에서 멀어질수록 값이 작아지는 정도가 큼) -> 블러링 효과는 커짐
- 깂이 작을 수록 (대상 점에서 멀어질수록 값이 작아지는 정도가 작음) -> 블러링 효과는 작아짐.

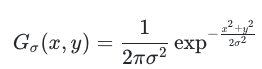
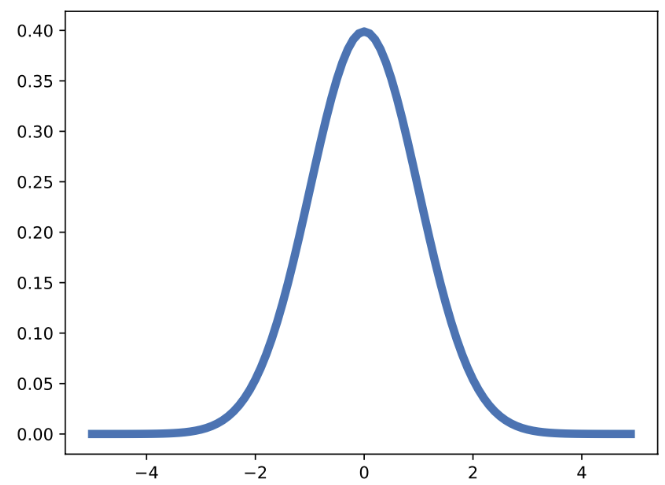


Low-pass / High-pass의 기본 개념
- Low-pass filter(LPF)는 저주파 성분을 통과시키고 고주파를 억제한다.
영상에서는 완만한 밝기 변화를 보존하고 급격한 변화(에지, 디테일)를 줄이므로 블러링 효과가 난다. - High-pass filter(HPF)는 고주파 성분을 통과시키고 저주파를 억제한다.
영상에서는 에지·세부 디테일을 강조하고, 평탄 영역은 줄어든다.

가우시안 필터는 대표적인 Low-pass이다
- 2D 가우시안 커널은 다음과 같다.
\(G_\sigma(x,y)=\frac{1}{2\pi\sigma^2}\exp!\left(-\frac{x^2+y^2}{2\sigma^2}\right)\) - 이 커널로 영상을 컨볼루션하면 저주파가 통과하고 고주파가 감쇠하므로 블러링이 발생한다.
- 주파수영역에서 가우시안의 푸리에변환도 가우시안 형태이므로 이상적인 저역통과 특성을 부드럽게 근사한다. σ가 커질수록 컷오프가 더 낮아져 더 많이 흐려진다.
원본 − 블러 = 디테일(High-pass 성분)이다
- 원본 영상 (I)와 가우시안 블러 (I_{LP}=I*G_\sigma)가 있을 때,
디테일(고주파) 성분을
\(D = I - I_{LP}\)
로 정의한다. 이 연산이 고역통과(High-pass)에 해당한다. - 직관적으로 (I_{LP})는 완만한 배경만 남기고, 이를 원본에서 빼면 급격한 변화(에지, 질감)만 남는다.
Sharpening의 원리: Unsharp Masking / High-boost
- Unsharp masking은 디테일 (D)를 원본에 더하는 방식의 샤프닝이다.
\(I_{sharp} ;=; I + k \cdot D ;=; I + k,(I - I_{LP})\) - (k=1)이면 전형적인 언샤프 마스킹이다. (k>1)이면 High-boost filtering이라 하며, 디테일을 더 강하게 부스트한다.
- 등가식으로 정리하면 하나의 합성 커널로도 표현된다.
\(I_{sharp} ;=; (1+k),I ;-; k,I_{LP}\)
즉, 저주파를 빼고 고주파를 강화하는 구조이다.
5. Laplacian 기반 샤프닝과의 관계
- Laplacian은 2차 미분 연산자이며 고주파 강조 성질을 가진다.
[
\nabla^2 I \approx
\begin{bmatrix}
0 & -1 & 0\
-1 & 4 & -1\
0 & -1 & 0
\end{bmatrix}
- I
\quad\text{또는}\quad
\begin{bmatrix}
-1 & -1 & -1\
-1 & 8 & -1\
-1 & -1 & -1
\end{bmatrix} - I
]
- 샤프닝을 (I_{sharp}=I - \lambda \nabla^2 I)로 구현하기도 한다.
- DoG(Difference of Gaussians) (G_{\sigma_1}-G_{\sigma_2})는 **LoG(Laplacian of Gaussian)**을 근사하므로, 가우시안 두 개의 차로도 에지/디테일 강조를 구현한다.
주파수영역 관점 요약
- 가우시안 LPF의 주파수 응답 (H_{LP}(u,v))는 중심(저주파)에서 크고 바깥(고주파)으로 갈수록 작아진다.
- HPF는 (H_{HP}(u,v)=1-H_{LP}(u,v))로 생각할 수 있다. 공간영역에서 보면 (I - I_{LP})와 동일한 형태가 된다.
- 언샤프 마스킹은 (H_{USM}(u,v)=1+k,[1-H_{LP}(u,v)])의 주파수 응답을 갖는다. 즉, 저주파는 거의 유지하고 고주파를 배율 (k)만큼 증폭한다.
실무 팁과 파라미터 선택
- 가우시안 σ 선택
- σ가 작을수록 미세한 노이즈까지 디테일로 취급되어 샤프닝 시 노이즈도 키워진다.
- 항공/자연 이미지에서는 σ≈1.0~2.0이 안정적이다. 큰 σ로 블러한 뒤 빼면 좀 더 굵은 구조만 강조된다.
- 샤프닝 강도 k(또는 λ) 선택
- (k)를 0.3~1.0 정도로 시작한다.
- 너무 크면 halo(윤곽선 과장), 링잉, 오버슈트가 발생한다.
- 채널 처리
- 컬러 영상은 보통 **YUV/YCbCr의 Y(휘도)**만 샤프닝한다. RGB 채널별 샤프닝은 색 노이즈와 색번짐을 유발하기 쉽다.
- 노이즈 주의
- HPF/샤프닝은 노이즈도 고주파로 취급하여 함께 증폭한다.
- 노이즈가 큰 경우 약한 denoise 후 샤프닝이 안전하다(예: 비등방성 확산, Bilateral, NL-means).
- 경계/패딩
- 컨볼루션 시 zero-padding은 가장자리 어둠/밝음 왜곡을 낳기 쉽다. reflect/border replicate 패딩을 권장한다.
절차
- (I)에 가우시안 LPF를 컨볼브하여 (I_{LP})를 얻는다 → 블러 영상이다.
- 디테일 (D=I-I_{LP})를 계산한다 → HPF 결과이다.
- 샤프닝 (I_{sharp}=I+kD)를 적용한다 → 선명한 영상이다.
- (k,\sigma)를 조정하며 노이즈 증폭과 halo를 최소화하도록 튜닝한다.
정리
- 가우시안 필터는 저역통과라서 블러를 만든다.
- 원본 − 블러 = 디테일이므로 이 연산이 고역통과이다.
- 원본 + 디테일×계수를 하면 샤프닝이 된다.
- 파라미터(σ, k)와 채널/패딩/노이즈 처리를 적절히 선택하면 안정적으로 선명화를 구현할 수 있다.
(2) Motion blur
원리
특정 방향(각도 θ)과 길이 L만큼 이동 평균을 취하는 커널을 만든다.
\(h(x,y) = \begin{cases} 1/L, & \text{if } (x,y) \text{가 방향 } \theta \text{선상에 있을 때}\ 0, & \text{otherwise} \end{cases}\)
코드
def make_motion_kernel(length=15, angle=0):
"""길이와 각도를 가진 motion blur kernel 생성"""
kernel = np.zeros((length, length))
center = length // 2
rad = np.deg2rad(angle)
# 선을 따라 1을 찍기
for i in range(length):
x = center + int((i - center) * np.cos(rad))
y = center + int((i - center) * np.sin(rad))
if 0 <= x < length and 0 <= y < length:
kernel[y, x] = 1
kernel /= np.sum(kernel)
return kernel
def apply_motion_blur(img, length=15, angle=30):
kernel = make_motion_kernel(length, angle)
blurred = cv2.filter2D(img, -1, kernel)
return np.clip(blurred, 0, 1)
reference
'AI > Computer Vision' 카테고리의 다른 글
| [CV] FFT란 Fast Fourier Transform (0) | 2025.10.16 |
|---|---|
| [CV] Image Processing 개념 총정리! / Image degradation 직접 구현 -②③ (Blur, Periodic Noise, Low Contrast) (0) | 2025.10.16 |
| [CV] Diagonal Gaussian Distribution 설명 (0) | 2025.09.29 |
| [CV] Watermark 논문 정리 모음 (0) | 2025.09.24 |
| [CV] conditional, unconditional image generation / ImageNet class label diffusion 어떻게 이용 (0) | 2025.09.08 |