[CV] Image Processing 개념 총정리! / Image degradation 직접 구현 -②③ (Blur, Periodic Noise, Low Contrast)

AI/Computer Vision

[CV] Image Processing 개념 총정리! / Image degradation 직접 구현 -②③ (Blur, Periodic Noise, Low Contrast)

도도걸만단 2025. 10. 16. 18:35

저번에 gaussian blur에 대해 알아보았다. 다음 내용을 보고 오면 이해가 편하다.

참조 :

https://minsunstudio.tistory.com/103

[CV] Image degradation 직접 구현 -① (Blur, Periodic Noise, Low Contrast)

① Blur, ② Periodic Noise, ③ Low Contrast의 세 가지 degradation를 library 없이!!! 직접 구현하는 정석적인 방법시작 전나는 Inria Aerial Image Labeling Dataset에서 gt를 골라서 사용하겠다.https://minsunstudio.tistory.com

minsunstudio.tistory.com

https://minsunstudio.tistory.com/105

[CV] FFT란 Fast Fourier Transform

영상에서 샘플링(sampling)이란, 연속적인(아날로그) 영상을 이산적인(디지털) 데이터로 변환할 때 공간적으로 일정 간격으로 신호를 추출하는 과정을 말한다.1. 기본 개념실제 세상에서 빛이 물체

minsunstudio.tistory.com

computer vision 의 기초내용 총정리 한 기록용 글.

들어가기 앞서 정리

1. Python library 사용

type	library
FFT, IFFT	np.fft.fft2, np.fft.ifft2, np.fft.fftshift
필터링	scipy.signal.convolve2d, cv2.filter2D
Wiener	scipy.signal.wiener
Histogram Equalization	cv2.equalizeHist, cv2.createCLAHE
Edge Detection	cv2.Canny
Hough Transform	cv2.HoughLines, cv2.HoughLinesP
Visualization	matplotlib.pyplot.imshow, plt.hist

2. process

type	type
Degradation 생성	Blur, Noise, Contrast 조절
Restoration	Wiener, Filtering, HE
Enhancement	Histogram Equalization, Sharpening
Analysis	FFT, Canny, Hough, PSNR/SSIM

Comprehensive Overview for Computer Vision 총 정리 !!!! (길어요)

컴퓨터 비전 개요
- Vision System = “세상을 보는 인공지능”
- 이미지 처리는 그 기반 단계로, 데이터를 다루기 전에 신호(signal) 로 이해해야 함.
- 즉, 비전 과제의 시작은 “이미지를 데이터로 표현하는 방법”을 아는 것.

Image & Image Data

이미지란?
- 픽셀 (pixel) = 2D 격자(행렬 matrix)의 한 점.
- 각 픽셀은 밝기(intensity) 또는 색상(color value)을 갖는다.
아날로그 → 디지털 변환
- 아날로그 신호는 연속적이고, 디지털은 이산적.
- 디지털 이미지는 2D 배열 (matrix) 형태로 표현.
디지털 이미지 활용 3단계
1. 저장(Storage)
2. 처리(Processing)
3. 전송(Transmission)

Image and Resolution

해상도(Resolution): 이미지의 세부 정보 수준을 결정.
픽셀 수가 많을수록 더 세밀한 정보 표현 가능.
즉, 해상도는 인식 능력과 직접 연관됨.

Image Signal & Spatial Frequency

영상(Image) = 신호(Signal)
- 아날로그 신호: 연속 변화.
- 디지털 신호: 샘플링 (sampling)으로 이산화.

Spatial Frequency (공간 주파수)

영상의 밝기 변화 빈도.
- 낮은 주파수 → 완만한 변화 (배경, 큰 패턴).
- 높은 주파수 → 급격한 변화 (에지, 디테일).
Fourier Transform: 영상 신호를 주파수 성분으로 분해해 분석.
- 각 주파수가 영상에 얼마나 기여하는지 알 수 있음.

🔹 Interpolation (보간) / Resizing

Upsampling (확대): 픽셀 사이에 새 값을 추정해 넣음.
Downsampling (축소): 일부 픽셀만 남기기 때문에 정보 손실 발생.
Ideal Low Pass Filter: 리사이징 시 aliasing (위조 주파수) 제거에 사용.
- 실제로는 무한대 kernel (sinc 함수)을 근사한 필터를 사용.

🔹 Nyquist Sampling 정리

정확히 복원하려면 최대 주파수의 두 배 이상 샘플링해야 함.
부족하게 샘플링하면 aliasing (거짓 패턴) 발생.

🔹 Interpolation 유형

Bilinear Interpolation : 주변 4픽셀 평균.
Bicubic Interpolation : 16픽셀 이용, 더 부드럽고 고품질.

Image Quantization (영상 양자화)

🔹 정의

연속 밝기 값을 유한한 레벨로 변환하는 과정.
- 예: 256단계(8bit), 4096단계(12bit) 등.
영상 센서가 빛의 세기를 전압으로 변환하고, 이를 디지털 수로 표현.
- Dynamic range = 전압이 표현할 수 있는 범위.

🔹 비트 깊이

4 level (2bit): 밴딩(banding) 현상 심함.
8bit (256 gray levels): 일반 영상 표준.
12bit 이상: 의료 영상(DICOM, NIfTI)에서 필수 — 진단 정확도 향상.

이미지에서 비트의 의미

이미지의 한 픽셀(pixel) 은 밝기값(혹은 색상값)을 숫자로 표현
이때, 그 숫자를 표현하기 위해 사용하는 비트 수를 ‘비트 깊이(bit depth)’

비트 깊이 (bit depth) = 한 픽셀이 표현할 수 있는 밝기 단계 수(Gray level) 를 의미

1bit	2단계 (0~1)	흑/백	완전한 흑백 이미지
2bit	4단계 (0~3)	0, 85, 170, 255	밝기 표현이 거칠고 계단 현상(banding)
8bit	256단계 (0~255)	자연 영상 대부분	매끄럽고 연속적인 밝기 표현
12bit	4096단계	의료 영상(DICOM 등)	매우 세밀한 밝기 구분 (예: MRI, CT)
16bit	65,536단계	과학/위성 영상	물리량 정밀 측정용

밴딩(Banding) 현상

비트 수가 적어서 밝기 단계가 뚜렷하게 끊겨 보이는 현상

예시:

하늘처럼 밝기 변화가 부드러운 부분을 2bit (4단계)로 표현하면,매끄럽게 연결되지 않고 계단처럼 층이 생긴다.
8bit로 표현하면 256단계로 세밀하므로 이런 현상이 거의 안 보임

🔹 Quantizer 종류

Uniform Quantizer : 등간격 양자화.
Lloyd–Max Quantizer : MSE (평균제곱오차)를 최소화하도록 적응형 양자화.
- (u): 원본 신호, (u'): 양자화 결과.
- 반복적으로 오차 계산 → 수렴할 때까지 갱신.
Vector Quantization : 픽셀 단독이 아닌 인접 픽셀 벡터를 한꺼번에 양자화하여 공간 상관성 활용.

Image Enhancement (영상 향상)

영상의 시각적 품질을 개선하거나 특정 정보를 강조하는 처리.

🔹 (24) Contrast Stretching

입력 밝기 범위를 확장하거나 축소.
예: [50, 180] → [0, 255]로 매핑 → 대비 강화.
약한 대비 → 강조(Emphasis)
너무 강한 대비 → 약화(Weakening).

🔹 (25) Gamma Correction

밝기 보정.
- 감마 값 > 1 → 어두운 영역 더 밝게.
- 감마 값 < 1 → 밝은 영역 더 어둡게.
인간 눈의 비선형 응답을 보정하기 위함.

🔹 (26) Intensity Level Slicing

특정 회색 레벨 범위를 강조.
예: 의료 영상에서 조직 특정 밝기 영역 만 분리.
Binary mask 형태 가능 (white/black 값만 남김).

🔹 (27) Image Subtraction / Change Detection

두 시간대의 영상 차이를 계산하여 변화 감지.
- 의료: 혈류 변화 추적.
- 산업: 모션 검출, 변화 영역 분석.

🔹 (28–29) Histogram Equalization

히스토그램: 영상의 밝기 분포.
목표: 밝기 값을 균등하게 분포시켜 대비 향상.
CDF (누적 분포 함수)를 이용해 재매핑.
어두운 영상에서 밝기 분포를 펼치는 효과.

🔹 (30–36) Spatial Filtering (공간 필터링)

① Mean Filtering

주변 픽셀의 평균값 적용 → 노이즈 제거.
커널(윈도우) 크기에 따라 효과 결정.

② Median Filtering

주변 픽셀 중 중간값 선택.
Salt-and-pepper noise (점잡음)에 강함.

③ Unsharp Masking / Crispening

원본 영상에서 블러된 버전 빼기 → 에지 강조.
선명하지만 노이즈도 함께 증폭됨.

④ Edge Enhancement

에지 강화용 필터 (예: Sobel, Laplacian).
메디컬 영상에서 윤곽선 강조에 활용.

🔹 (37–38) Multispectral Image Enhancement

다양한 파장대(Visible + IR 등) 영상 결합.
Log Ratio, PCA 등을 이용해 정보량 증가.

🔹 (38) False Color vs Pseudo Color

False Color : 단일 밴드 (흑백) 영상에 색상 맵 입힘.
Pseudo Color : 여러 밴드 (다중 스펙트럼) 정보 결합 → 더 의미 있는 색 표현.

Image degradation

Blur — Gaussian 또는 Motion blur 중 하나를 택해서 영상 전체를 흐리게 한다.
→ 대기 흐림이나 카메라 흔들림을 모사한다.
Periodic Noise — 사인파(sinusoidal) 패턴을 더해서 전자 간섭(electronic interference)을 흉내낸다.
→ FFT 분석에서 보게 될 스파이크가 여기서 생긴다.
Low Contrast — 픽셀의 dynamic range를 줄인다.
→ 센서 노후나 조명 불균형으로 인한 대비 저하를 표현한다.

영상 처리의 기본 과정

입력 영상 → 전처리 → 분할 → 표현 및 설명 → 인식 및 해석 → 결과

영상 처리 기법

(1) 영상 향상 (Image Enhancement)

목적:
사람이 보기 쉽거나, 후속 분석이 잘 이루어지도록 영상의 시각적 품질을 높이는 것이다.

주요 기술:

대비 향상(Contrast enhancement): 명암 분포를 넓혀 선명하게 만든다.
에지 향상(Edge enhancement): 경계 부분의 변화량을 강조한다.
히스토그램 평활화(Histogram equalization): 픽셀 밝기 분포를 균등하게 조정한다.
의사 컬러링(Pseudo coloring): 흑백 영상에 인위적으로 색을 입혀 가시성을 높인다.
잡음 제거(Noise filtering): Gaussian, Median, Bilateral 등 필터를 이용해 노이즈를 줄인다.
에지 강조(Edge sharpening): Unsharp masking 등으로 경계를 선명하게 만든다.
스무딩(Smoothing): 세부 노이즈를 완화하여 전체 윤곽을 부드럽게 만든다.

(2) 영상 복원 (Image Restoration)

목적:
이미 열화(degradation)된 영상에서 손상 원인을 역으로 추정하여 원래 영상에 가깝게 복구하는 것이다.

주요 기술:

선명화(De-blurring): 블러(흐림) 성분을 제거한다.
잡음 제거(Noise filtering): 센서 노이즈나 전자 간섭을 제거한다.
기하학적 왜곡 보정(Correction of geometric distortion): 렌즈 왜곡, 기울어짐 등을 보정한다.
역필터링(Inverse filtering): 주파수 영역에서 시스템의 전달함수를 역으로 적용해 원본 신호를 복원한다.

- with a small(wide) spread → low(high) contrast

- 히스토그램의 분포가 넓을 경우, 대비가 큰 것(좋은 것). 히스토그램의 분포가 좁을 경우, 대비가 낮은 것.

Histogram Equalization

- Histogram equalization is a method in image processing of contrast adjusment using the image's histogram.

히스토그램이란 ?

히스토그램은 영상의 밝기(intensity) 또는 명암 값의 분포를 보여주는 일종의 빈도표(frequency table)이다.

영상의 모든 픽셀을 0~255 범위의 값으로 표현할 수 있다.
각 밝기 값이 몇 개의 픽셀에서 나타나는지를 세어, 막대그래프로 표현한 것이 히스토그램이다.
x축은 밝기 값(0은 검정, 255는 흰색), y축은 해당 밝기 값의 픽셀 개수를 의미한다.

예를 들어,
영상의 대부분이 어두운 부분(0~50)에 몰려 있으면 그래프가 왼쪽에 몰려 있고, 밝은 부분이 많으면 오른쪽에 몰려 있는 형태가 된다.

그래프가 좁은 구간에 몰려 있다면 Low Contrast, 넓게 퍼져 있다면 Normal Contrast로 판단한다.

수학적으로는 다음을 수행한다:

영상의 모든 픽셀 값을 읽는다.
0~255(또는 0~1 정규화된 값)의 구간을 256개의 bin으로 나눈다.
각 bin에 해당하는 픽셀 개수를 센다.
이를 리스트 또는 배열 형태로 저장한다.

즉, 픽셀 값의 분포를 수치로 세어 통계화하는 것이 히스토그램을 계산한다는 의미이다.

왜 이걸 해야 하는가

히스토그램을 계산하면 다음과 같은 판단이 가능하다.

Low Contrast 영상은 히스토그램이 좁은 영역에 몰려 있다.
→ 밝기 값이 특정 범위에 집중되어 있으므로 전체적으로 탁하고 밋밋하다.
High Contrast 영상은 히스토그램이 넓게 퍼져 있다.
→ 어두운 부분과 밝은 부분이 함께 존재하므로 선명하다.

즉, 히스토그램을 계산하면 이 영상이 얼마나 넓은 밝기 범위를 사용하고 있는가를 객관적으로 알 수 있다.

② Periodic Noise (Sinusoidal pattern 추가)

주기를 가지는 Noise.
DFT를 한 주파수 도메인에서 일정한 패턴을 확인할 수 있다.

Periodic noise

주기적 노이즈(Periodic noise)는 영상이 촬영되는 과정에서 전기적 간섭(electrical interference)으로 인해 발생하는 경우가 많다.

마치 어떤 반복적인 패턴이 덧씌워진 것처럼 보인다.

이 현상을 주파수 영역에서 살펴보면, 영상의 푸리에 스펙트럼 상에 일정한 위치에 밝은 점(이산적인 스파이크)들이 나타난다.

이러한 스파이크는 주기적 신호(사인파 형태의 간섭)가 영상 전체에 퍼져 있음을 의미한다.

원리

공간좌표 (x, y)에 대해 주기적으로 진동하는 신호를 더한다.
\(n(x,y) = A \sin(2\pi(f_x x + f_y y) + \phi)\)

(A): 노이즈의 진폭
(f_x, f_y): 주파수 (이미지 크기 대비 0.05~0.15 정도 추천)
(\phi): 위상(0~2π 사이 값)

코드

def add_periodic_noise(img, fx=0.08, fy=0.05, A=0.2, phi=0):
    """사인 파형을 이용한 periodic noise 추가"""
    h, w = img.shape[:2]
    X, Y = np.meshgrid(np.arange(w), np.arange(h))
    sinusoid = A * np.sin(2*np.pi*(fx*X + fy*Y) + phi)
    if img.ndim == 3:
        sinusoid = np.repeat(sinusoid[..., None], 3, axis=2)
    noisy = img + sinusoid
    return np.clip(noisy, 0, 1)

이 노이즈는 나중에 FFT에서 주기적 스파이크로 확인할 수 있다.

③ Low Contrast (Dynamic range 축소)

영상처리에서 이미지의 밝은 부분과 어두운 부분의 명도 차이가 크지 않아 전반적으로 흐릿하고 선명도가 떨어져 보이는 현상을 의미

Low Contrast란 영상의 밝기 값이 좁은 범위에 몰려 있어 밝고 어두운 영역의 구분이 약해진 상태를 말한다.

시각적으로는 탁하고 납작해 보이며, 에지와 질감 같은 고주파 성분이 두드러지지 않는다.

알고리즘 관점에서는 특징점 추출, 에지 검출, 분할, 매칭 등의 성능이 저하되기 쉽다.

원인

조명 부족 또는 조명 범위가 좁음
센서 감응도 저하, 노출 부정확, 렌즈/대기 산란에 의한 감쇠
후처리 단계의 동적 범위 압축, 톤매핑 오류
강한 안개, 연무, 수중 환경 등 전역 감쇠 매체 존재
JPEG 등 손실 압축 후 로컬 대비 약화

특징
- 회색조에 가까운 이미지: 이미지의 픽셀값(명도) 분포가 좁은 범위에 몰려 있어, 전체적으로 어둡거나 밝은 영역의 구분이 명확하지 않습니다.
- 디테일 부족: 밝은 영역과 어두운 영역의 경계가 뚜렷하지 않아 사물의 윤곽선이나 세부적인 특징을 알아보기 어렵습니다. 정보 손실: 대비가 낮아지면서 이미지에 포함된 시각적 정보가 줄어들어, 객체 인식이나 분석과 같은 작업의 정확도를 떨어뜨릴 수 있습니다.
발생 원인
- 환경적 요인: 안개가 끼거나 역광인 상황, 또는 전체적으로 빛이 부족한 저조도 환경에서 촬영한 이미지에서 자주 발생합니다.
- 촬영 장비: 카메라의 성능이나 설정이 부적절할 때 저대비 이미지가 나올 수 있습니다.
- 압축 과정: 이미지 파일을 압축하거나 변환하는 과정에서 대비가 손실될 수 있습니다.
보정 방법
- 영상처리에서는 저대비 문제를 해결하기 위해 다양한 기법을 사용합니다.
- 히스토그램 평활화(Histogram Equalization): 이미지의 픽셀값 분포(히스토그램)를 전체 명도 범위에 걸쳐 균일하게 분포되도록 조정하여 대비를 개선하는 방법입니다.
- 대비 확장(Contrast Stretching): 이미지의 최소 명도와 최대 명도를 전체 명도 범위(예: 0~255)에 맞게 늘려줌으로써 대비를 확장하는 방법입니다.
- 딥러닝 기반 보정: 최근에는 저조도 이미지의 밝기와 대비를 동시에 개선하는 딥러닝 기반 기술이 활발히 연구되고 있습니다.

원리

픽셀의 최소–최대 범위를 중간으로 압축한다.
\(I'(x,y) = \alpha I(x,y) + \beta, \quad \alpha < 1\)
예를 들어 α=0.6, β=0.2이면, 원래 [0,1] 범위의 값이 [0.2,0.8]로 줄어든다.

코드

def reduce_contrast(img, alpha=0.6, beta=0.2):
    """명암 대비 축소"""
    low_contrast = alpha * img + beta
    return np.clip(low_contrast, 0, 1)

=>세 가지를 순서대로 적용한 전체 예시

from tifffile import imread
import matplotlib.pyplot as plt

# 1. 이미지 불러오기
img = imread("AerialImageDataset/train/images/austin1.tif").astype(np.float32)
img /= 255.0  # 정규화

# 2. Blur 적용 (Gaussian or Motion)
blurred = apply_gaussian_blur(img, sigma=2.0)
# blurred = apply_motion_blur(img, length=13, angle=30)

# 3. Periodic noise 추가
noisy = add_periodic_noise(blurred, fx=0.08, fy=0.05, A=0.15, phi=0)

# 4. Contrast 축소
degraded = reduce_contrast(noisy, alpha=0.6, beta=0.2)

# 5. 결과 저장
cv2.imwrite("degraded.png", (degraded * 255).astype(np.uint8))

# 6. 단계별 시각화
fig, axes = plt.subplots(1, 4, figsize=(20,5))
axes[0].imshow(img); axes[0].set_title("Original")
axes[1].imshow(blurred); axes[1].set_title("Blurred")
axes[2].imshow(noisy); axes[2].set_title("With Periodic Noise")
axes[3].imshow(degraded); axes[3].set_title("Low Contrast (Final)")
for ax in axes: ax.axis("off")
plt.show()

1. Blur	Gaussian 또는 Motion blur 적용	σ 또는 (L, θ)	step1_blur.png
2. Periodic Noise	Sinusoidal 패턴 추가	A, fx, fy, φ	step2_periodic.png
3. Low Contrast	Dynamic range 축소	α, β	degraded.png (최종)

Notch filter

이러한 Periodic noise를 제거하는 대표적인 방법은 주파수 영역에서 노치 필터(notch filter) 를 적용하는 것이다.

노치 필터는 스파이크가 존재하는 특정 주파수 대역만 선택적으로 제거하는 방식으로, 신호의 나머지 부분에는 영향을 최소화하면서 해당 주파수의 간섭 성분만 억제한다.

노치 필터를 적용하면 주기적 노이즈가 상당히 줄어든 결과를 얻을 수 있다. 다만, 필터링 후에도 영상의 경계 부분에는 잔여 노이즈가 남을 수 있다. 이 잔여 노이즈를 더 줄이기 위해 필터의 차단 폭을 넓히거나 추가적인 저역통과 필터(low-pass filter)를 적용할 수도 있다. 그러나 이 경우 미세한 디테일 정보까지 손실될 가능성이 높다.

즉, 노이즈 제거와 세부 정보 보존은 상충 관계(trade-off)에 있으며, 어느 쪽을 더 중시할지는 응용 목적에 따라 달라진다.

예를 들어, 영상 속 건물의 세부 질감이 중요하지 않다면 저역통과 필터로 경계 노이즈를 함께 제거하는 것이 적절할 수 있다.

반면, 세부 구조가 중요한 경우라면 경계 부분을 단순히 잘라내는(cropping) 방식이 더 나은 선택이 될 수 있다.

Band-reject filter (대역차단 필터) & Bandrepass filters (대역통과 필터)

1) Band-reject filter (대역차단 필터)

특정 주파수 대역만 차단하고 그 외의 주파수 성분은 통과시키는 필터
이는 주기적 노이즈(periodic noise) 제거에 매우 효과적이며, 모든 주파수를 통과시키는 올패스 필터(All-pass filter)의 여집합 개념으로 이해할 수 있습니다.
밴드-패스 필터(Band-pass filter)의 반대 역할을 합니다.

Periodic Noise Reduction

주기성을 가지는 Noise는 Frquency domain에 point로 나타나고, 이 그 point의 주파수 성분을 없애기 위해 원 형태(band) 또는 점(notch) 형태로 필터를 만든다.

2) Bandrepass filters (대역통과 필터)

특정 주파수 영역만 통과시키는 필터링
위의 예시로 적용하면 Noise만 보이게 된다.

FFT → Filtering → Wiener → HE → Canny → Hough

FFT (주파수 분석) [TO DO 1-(1)]
목적: 열화된 영상에서 주기적 노이즈의 위치를 찾는다.
하는 일: 영상의 푸리에 변환을 하고, magnitude 스펙트럼을 로그 스케일로 시각화한다. 중심 대칭의 밝은 점(스파이크)이 있으면 그것이 주기적 간섭 성분이다. 이 좌표를 기록한다.
입력/출력: 입력은 degraded 이미지(그레이스케일). 출력은 스펙트럼 이미지와 스파이크 좌표 목록이다.
Filtering (notch 또는 band-reject) [TO DO 1-(2)]
목적: FFT에서 찾은 주파수 성분만 선택적으로 제거한다.
하는 일: 스파이크 좌표를 중심으로 Gaussian/Butterworth 형태의 노치 필터를 만든다. 주파수 도메인에서 곱한 뒤 iFFT로 되돌려 공간 영상으로 복귀한다.
입력/출력: 입력은 스파이크 좌표와 degraded 스펙트럼. 출력은 주기 노이즈가 줄어든 영상이다.
주의: 너무 넓게 잘라내면 유용한 고주파까지 손실되어 에지가 약해진다.
Wiener (복원, 디블러) [TO DO 1-(2)]
목적: 블러를 역추정해 선명도를 회복한다.
하는 일: 사용자가 가한 블러(가우시안 σ 또는 모션 L, θ)로 PSF를 만들고, Wiener 필터
\hat{F} = H* / (|H|^2 + K) · G
를 적용한다. K는 SNR 역수에 해당하는 안정화 상수이다.
입력/출력: 입력은 노치 필터링 후 영상과 PSF, K. 출력은 블러가 완화된 영상이다.
주의: K가 너무 작으면 노이즈가 증폭되고, 너무 크면 디테일이 사라진다.
HE (Histogram Equalization, 대비 향상) [TO DO 1-(3)]
목적: 동적 범위를 넓혀 전체 대비를 개선한다.
하는 일: 전역 HE 또는 CLAHE로 밝기 분포를 재매핑한다. 보통 Y 채널만 처리한다.
입력/출력: 입력은 디블러 결과. 출력은 대비가 개선된 최종 복원 이미지이다.
주의: 노이즈가 함께 강조될 수 있어 과도한 평활화는 피한다.
Canny (에지 검출) [TO DO 2-(1)]
목적: 구조적 윤곽(도로 경계 등)을 안정적으로 검출한다.
하는 일: 가우시안 스무딩→그레이디언트 계산→비최대 억제→이중 임계 히스테리시스로 에지를 얻는다.
입력/출력: 입력은 복원·향상된 영상. 출력은 에지 맵이다.
주의: 임계값과 σ가 과도하면 도로가 끊기거나 노이즈가 에지로 남는다.
Hough (직선 검출) [TO DO 2-(1)]
목적: 에지 맵에서 직선(도로 축)을 검출한다.
하는 일: 누산기 공간(ρ, θ)에 에지 픽셀이 투표하여 피크를 직선으로 해석한다. Probabilistic Hough를 쓰면 분절된 선분을 직접 얻는다.
입력/출력: 입력은 Canny 에지. 출력은 검출된 선(혹은 선분) 집합이다.
이후 활용: 각도 히스토그램, 길이 합계, 밀도 등의 정량 분석으로 복원 효과를 평가한다.

왜 이 순서인가

FFT로 문제의 주파수 성분을 확인하고 좌표를 확보한다.
그 주파수만 우선 제거해야 이후 Wiener가 노이즈를 신호처럼 증폭하지 않는다.
블러를 복원한 뒤에
대비를 올려 구조적 정보를 더 분명하게 만든다.
그다음 에지 검출을 하면 잡음에 덜 민감하고 연결성이 좋아진다.
마지막으로 직선 검출과 방향 통계를 수행하면 도로 구조를 정량화할 수 있다.

Digital Image Processing (II)

Image Restoration 및 Filtering

핵심 주제 흐름:
Image Observation Model → Noise Model → Inverse Filtering → Wiener Filtering → Image Analysis (Edge/Boundary Extraction)

즉, 카메라나 센서 등에서 촬영된 영상이 왜 손상되는지부터 시작해,
이를 수학적으로 모델링하고 → 복원 필터를 통해 노이즈를 억제하고 원 영상을 재구성하는 과정을 다룸

① Image Observation Model (영상 관찰 모델)

영상이 만들어질 때 실제 세상에서 어떤 과정을 거쳐 디지털 데이터로 변환되는지를 모델링합니다.

관찰 모델:
\(g(x,y) = f(x,y) * h(x,y) + \eta(x,y)\)
- ( f(x,y) ): 원래 깨끗한 영상 (true image)
- ( h(x,y) ): 시스템의 임펄스 응답(impulse response) — 블러나 흐림을 유발하는 시스템 특성
- ( * ): convolution
- \( \eta(x,y) \): 노이즈(noise)

즉, 원본 영상이 시스템의 특성과 노이즈에 의해 변형되어 관측되는 것을 수식화한 형태
이후의 모든 복원(filtering) 기법은 이 수식을 기반으로 함.

② Noise Model (노이즈 모델)

영상에 포함된 노이즈(잡음)의 종류를 단순화하여 모델링합니다.

Additive Noise (가산형 노이즈): g = f + n
→ 대표적으로 Gaussian noise, uniform noise.

Multiplicative Noise (곱셈형 노이즈): g = f x n
→ Speckle noise (초음파, 레이더 영상 등에서 많이 발생).
영상의 신호 강도에 비례해 잡음 세기가 달라짐.

이러한 노이즈 특성을 이해해야 어떤 필터를 적용할지 결정할 수 있다.

③ Inverse Filtering (역필터링)

영상 복원의 가장 기초적인 접근법입니다.

목표:
흐려진 영상 ( g ) 로부터 원본 ( f ) 를 복원.
주파수 영역에서의 기본 관계는
\(G(u,v) = H(u,v)F(u,v)\)
따라서
\(F(u,v) = \frac{G(u,v)}{H(u,v)}\)
즉, 시스템 응답 ( H(u,v) ) 로 나누어 블러링을 역으로 보정합니다.
문제점:
- ( H(u,v) )이 0에 가까운 주파수에서는 분모가 작아 노이즈가 증폭됨.
- 실제 영상에서는 완벽히 역변환 불가능 → 노이즈에 매우 민감.

그래서 “이론적으로는 완벽하지만 실제로는 불안정한 복원법”으로 분류

④ Pseudo Inverse Filtering (의사 역필터)

위 문제를 완화하기 위해 ( H(u,v) )가 너무 작은 영역에서는 역필터 적용을 제한.
\(\hat{F}(u,v) = \begin{cases} \dfrac{G(u,v)}{H(u,v)}, & \text{if } |H(u,v)| > T \ G(u,v), & \text{otherwise} \end{cases}\)
Threshold ( T )를 두어 안정성 확보.

⑤ Wiener Filtering (위너 필터)

가장 많이 쓰이는 최적 복원 필터입니다.
노이즈와 원본의 통계적 특성을 함께 고려해서 MSE (Mean Squared Error) 를 최소화합니다.

위너 필터는 잡음이 섞인 원본 이미지를 복원하기 위한 선형 필터로, 복원된 이미지와 원본 이미지 사이의 평균 제곱 오차(MMSE, Minimum Mean Square Error)를 최소화합니다.

이는 이미지의 열화(blurring)와 잡음의 영향을 동시에 고려하여 최적의 복원 결과를 얻으려고 합니다.

따라서 위너 필터는 역 필터링보다 더 나은 복원 성능을 보이며, 이미지 복원 분야에서 널리 사용됩니다.

input signal 이 들어올 때, 신호만을 얻길 원하기 때문에 undesired interference 성분을 억제하는 필터를 설계하고자 함
wiener filter를 써서 원하는 소스 신호 의 특성 (characteristics)을 그대로 유지하면서 input signal에 포함된 interference를 필터링하여 없애는 시스템을 만들 때 사용

핵심 아이디어
- 노이즈를 완전히 제거하는 대신,
  원본 영상과의 평균 제곱 오차를 최소화하는 최적의 절충점을 찾음.
공식
\(H_w(u,v) = \frac{H^*(u,v)}{|H(u,v)|^2 + \frac{S_{\eta\eta}(u,v)}{S_{ff}(u,v)}}\)
- \( H^*(u,v) \): 복소켤레
- \( S_{\eta\eta} \): 노이즈 파워 스펙트럼
- \( S_{ff} \): 원 영상의 파워 스펙트럼
\( S_{\eta\eta}/S_{ff} \) = 노이즈 대 신호비 (Noise-to-Signal Power Ratio)
→ 값이 클수록 노이즈 억제 강하게, 작을수록 원 신호 보존.
효과:
- 노이즈가 많은 주파수 영역은 약화시키고
- 신호가 강한 부분은 유지 → 밸런스 있게 복원.

Wiener filter의 원리

목표: 잡음이 섞인 관측 이미지로부터 원본 이미지를 가장 가깝게 복원합니다.
최소 평균 제곱 오차(MMSE): 필터링의 목표는 복원된 이미지와 실제 원본 이미지 사이의 평균 제곱 오차를 최소화하는 것입니다.
고려 요소: 위너 필터는 이미지가 열화된 정도(열화 함수)와 잡음의 통계적 특성(통계적 정보)을 모두 고려합니다.
작동 방식: 복원 과정에서 단순히 열화 함수를 역으로 적용하는 '역 필터링'과 달리, 위너 필터는 잡음의 영향을 줄이는 데 효과적입니다.
필터링 과정에서 잡음과 원본 이미지가 서로 상관관계가 없다는 가정을 기반으로 합니다.

주요 특징

이미지 복원: 움직임이나 다른 요인에 의해 발생한 블러(blur)나 잡음을 제거하는 데 사용됩니다.
최적의 성능: 평균 제곱 오차(MSE) 관점에서 최적의 선형 필터로 알려져 있습니다.
통계적 정보 활용: 잡음과 원본 신호의 통계적 특성을 이용하여 필터의 계수를 계산합니다.
다양한 응용: 이미지 처리 외에도 신호 처리, 제어 시스템, 통신 등 다양한 분야에서 활용됩니다.

⑥ Restoration Flow

Observation	( g = f*h + n )	시스템 모델링
Inverse Filter	( F = G/H )	이상적 복원 (노이즈에 약함)
Pseudo-Inverse	(	H
Wiener Filter	( H^*/(	H
Output	Reconstructed Image	노이즈 제거 + 선명한 영상 복원

⑦ Image Restoration 이후: Image Analysis 연결

복원된 영상에서 이제 에지(edge) 나 경계(boundary) 를 검출할 수 있음.
이 흐름이 이후 Image Analysis (Edge Detection, Boundary Extraction) 로 이어짐.

핵심 문제	촬영 과정에서의 블러 + 노이즈
기본 수식	( g(x,y) = f(x,y)*h(x,y) + \eta(x,y) )
Inverse Filter	단순한 역연산 — 노이즈에 매우 민감
Pseudo-Inverse Filter	작은 주파수에서 역필터 억제
Wiener Filter	통계적으로 최적(MSE 최소화) 복원
응용 분야	의료영상 복원, 위성영상 보정, CCTV 영상 복원 등

에지(Edge) 검출의 개념과 원리

1. 에지(Edge)란 무엇인가

에지(edge)는 영상에서 픽셀 값이 급격하게 변하는 경계 부분을 의미한다.
사람의 시각에서 물체의 윤곽이 구분되어 보이는 이유는 밝기(intensity)나 색상(color)의 변화 때문이다.
컴퓨터도 동일하게, 픽셀 값의 변화 정도(밝기 변화율)를 계산하여 테두리를 인식할 수 있다.

2. 픽셀 값 변화율과 미분(derivative)

이미지는 RGB 값 또는 밝기 값으로 이루어진 이산적인 2차원 행렬이다.
밝기 값이 빠르게 변하는 부분은 **밝기 함수의 기울기(gradient)**가 큰 부분이다.
따라서 픽셀 값의 변화율, 즉 미분값이 큰 곳을 에지로 판단한다.

연속 함수라면 다음과 같은 일반 미분식으로 표현할 수 있다.
\(f'(x) = \frac{df}{dx}\)

이 미분값의 절댓값이 어떤 임계값 (T)보다 크면,
\(|f'(x)| > T \quad \Rightarrow \text{edge로 판단한다.}\)

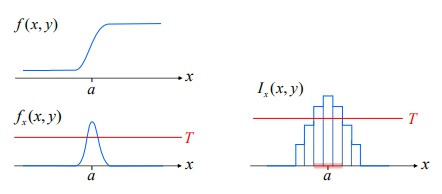
3. 이산 영상에서의 미분 근사화 (Discrete Differentiation)

하지만 컴퓨터에서의 이미지는 연속 함수가 아니라 이산 함수이므로
수학적인 미분을 그대로 적용할 수 없다.
대신 차분(difference)을 이용한 미분 근사화(finite difference approximation)를 사용한다.

1차원 이산 함수 ( f(x) )의 미분 근사는 다음 세 가지 방법으로 표현할 수 있다.

전진 차분 (Forward difference)	\(( f'(x) \approx \frac{f(x+1) - f(x)}{h} )\)	간단하지만 오차가 큼
후진 차분 (Backward difference)	\(( f'(x) \approx \frac{f(x) - f(x-1)}{h} )\)	유사하게 단순
중앙 차분 (Central difference)	\(( f'(x) \approx \frac{f(x+1) - f(x-1)}{2h} )\)	정확도 높고 대칭적

여기서 ( h )는 픽셀 간 간격을 의미하며, 영상에서는 일반적으로 ( h = 1 )로 둔다.
중앙 차분이 양쪽 픽셀을 모두 고려하므로 노이즈에 강하고,
에지 검출에서 가장 널리 사용된다.

4. 1차원 미분 마스크 (Difference Mask)

중앙 차분은 필터 형태로도 표현할 수 있다.
예를 들어 1차원 미분 마스크는 다음과 같다.

x 방향 미분 마스크: [-1, 0, 1]

이 마스크를 영상의 각 위치에 컨볼루션(convolution)하면,
해당 위치의 밝기 변화율(기울기)을 근사적으로 계산할 수 있다.

5. 2차원 영상에서의 미분

이미지는 가로(x)와 세로(y) 방향으로 이루어진 2차원 신호이므로,
에지를 구하기 위해서는 두 방향에 대한 **편미분(partial derivative)**을 각각 구해야 한다.
이를 ( G_x, G_y )라 하면 다음과 같다.

\(G_x = \frac{\partial f}{\partial x}, \quad G_y = \frac{\partial f}{\partial y}\)

각 방향에 대한 미분 결과를 결합하면 **그레이디언트(Gradient)**가 된다.

\(|\nabla f| = \sqrt{G_x^2 + G_y^2}\)

이 값이 일정 임계값 (T)보다 크면 해당 픽셀을 에지로 판단한다.
즉,
\(|\nabla f(x, y)| > T \quad \Rightarrow \text{Edge point}\)

6. 2차원 미분 마스크와 Sobel 연산자

2차원 영상의 잡음을 줄이기 위해,
실제 에지 검출에서는 단순한 1×3 마스크 대신 3×3 크기의 미분 마스크를 사용한다.
대표적인 예가 Sobel, Prewitt, Roberts 연산자이다.

Sobel 미분 마스크 (3×3)

x 방향:
\(\begin{bmatrix} -1 & 0 & 1\ -2 & 0 & 2\ -1 & 0 & 1 \end{bmatrix}\)

y 방향:
\(\begin{bmatrix} 1 & 2 & 1\ 0 & 0 & 0\ -1 & -2 & -1 \end{bmatrix}\)

이 마스크들은 중심 픽셀 주변의 이웃 픽셀 값을 고려하여
노이즈를 완화하면서 방향별 변화량을 추정한다.
즉, Sobel은 평활화(Smoothing)와 미분(Gradient)을 동시에 수행하는 효과가 있다.

위의 3가지 미분 마스크 중에서 대부분 edge detection에 Sobel 미분 마스크를 사용

에지 검출 과정 요약

이미지를 그레이스케일로 변환한다.
노이즈를 줄이기 위해 가우시안 블러 등을 적용한다.
x, y 방향 Sobel 마스크로 각각 미분한다.
그레이디언트 크기를 계산한다.
그레이디언트 크기가 임계값보다 큰 픽셀을 에지로 분류한다.

이 과정을 통해 영상의 경계선, 윤곽선, 물체의 구조를 정량적으로 검출할 수 있다.

Canny edge detector

Canny는 “좋은 에지 검출기”의 세 기준을 만족하도록 설계된다.

검출률 최대화(Detection): 진짜 에지는 놓치지 않게 한다.
정확한 위치(Localization): 검출된 에지의 위치 오차를 최소화한다.
단일 응답(Minimal Response): 하나의 에지에 대해 하나의 응답만 나오게 한다(이중 윤곽 방지).

이를 위해 노이즈 억제 → 그레이디언트 추정 → 비최대 억제(NMS) → 이중 임계+히스테리시스(연결 추적)의 4단계를 순차적으로 수행한다.

캐니 에지 검출 방법은 위에서 나온 3 x 3 크기의 소벨 마스크를 이용해 영상의 그레이디언트를 계산한 후, 그레이디언트의 크기와 방향을 모두 고려하여 정확한 에지 위치를 찾습니다.

또한 에지는 서로 연결되어 있는 가능성이 높다는 점을 고려해 그레이디언트 크기가 작게 나오는 에지도 놓치지 않고 찾을 수 있습니다.

Lena 원본 사진 :

DoG 연산에 대한 결과로 x 방향과 y 방향에 대한 결과값을 더하여 Gradient magnitude를 뽑아낸 결과 :

캐니 에지 검출 시 입력 영상으로 컬러 영상을 입력하면 RGB 각각의 픽셀값에 대해서 전부 미분하기 때문에 계산량을 줄이기 위해서 흑백으로 바꿔서 입력하는 것이 좋다.

Canny Edge Detection과의 관계

Canny 알고리즘은 이러한 Sobel 기반의 그레이디언트 검출을 포함한 고도화된 에지 검출기이다.
즉, Canny는 기본적으로 다음을 포함한다.

가우시안 필터로 노이즈 제거
Sobel로 그레이디언트 계산
비최대 억제(NMS)
이중 임계값과 히스테리시스(연결 추적)

따라서 Sobel은 Canny의 내부 구성요소이며,
대부분의 현대적인 에지 검출 알고리즘이 Sobel 기반의 미분 마스크를 사용한다.

에지(Edge)	픽셀 값이 급격히 변하는 경계 부분
원리	밝기 변화율(미분값) 계산 후, 큰 부분을 에지로 판단
미분 근사화	연속 미분 대신 중앙 차분(central difference) 사용
2D 처리	x, y 방향 편미분 후 gradient 계산
대표 연산자	Sobel, Prewitt, Roberts
응용 예시	Canny, Laplacian, Hough Transform 등

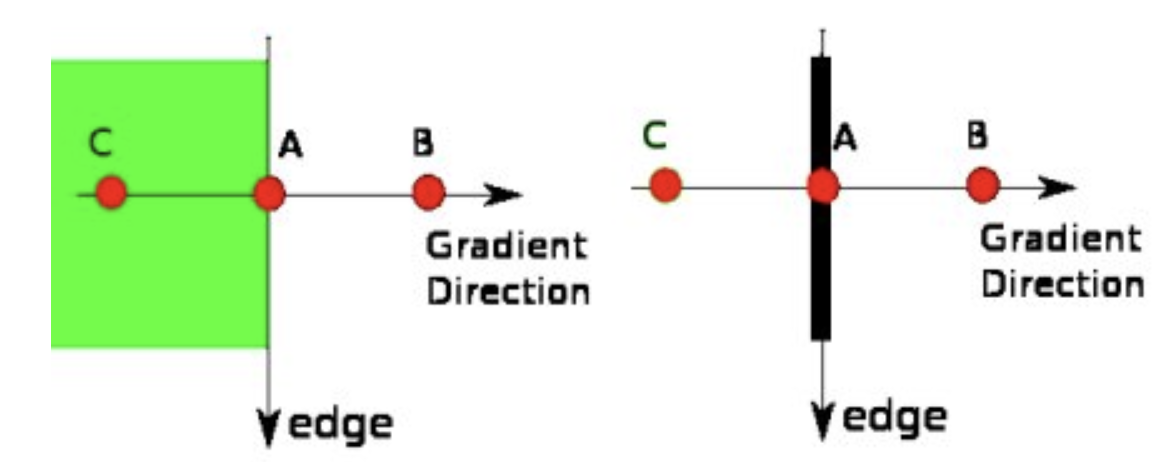
경계 중심으로 변하는 값이 크기 때문에 두꺼운 결과가 나오는 것이 문제임,

Non-max Suppression을 이용하면 다음과같이 선이 얇아질 수 있음.

허프 변환(Hough Transform)

영상에서 직선(line)이나 곡선(circle, ellipse 등) 같은 형태(geometry)를 검출하는 핵심 알고리즘
단순히 에지 검출보다 한 단계 높은 개념으로, 점들의 패턴 속에서 ‘형태의 존재’를 투표(voting)로 찾아내는 기법
영상에서 추출된 에지 정보를 사용해서 직선을 검출하는 방법

정의:
허프 변환(Hough Transform)은 이미지 공간(image space)의 점들을 모델 파라미터 공간(parameter space) 으로 변환하여
특정 형태(직선, 원 등) 를 찾는 방법이다.

영상에서 "이 점들이 한 직선(혹은 원)에 속하는가?"를 직접적으로 찾지 않고,
“이 점들이 어떤 파라미터 조합(θ,ρ)을 공통으로 갖는가?”를 통해 간접적으로 찾는 방식

기본 아이디어

(1) 이미지 공간에서의 점과 직선의 관계

직선 방정식:
y = ax + b

여기서 (a)는 기울기(slope), (b)는 절편(intercept).

→ 한 직선은 하나의 ((a,b)) 조합에 대응.
→ 하지만 한 점 (x₀, y₀) 는 무수히 많은 직선을 지날 수 있다 (즉, 무수한 (a,b) 값의 조합이 존재).

(2) 아이디어를 바꾸기

이제 반대로 ,

이미지 공간(image space)에서 한 점 (x₀, y₀) 은
파라미터 공간(parameter space)에서 무수한 직선으로 표현됨

b = -x₀ a + y₀

→ 이 식은 “(x₀, y₀)” 점을 지나는 모든 직선의 (a,b) 조합을 나타내는 선

그래서 여러 점을 이렇게 변환하면,

만약 여러 점이 하나의 직선을 공유한다면,
이 점들이 만든 여러 “b = -x₀a + y₀” 선들은 (a,b) 공간에서 한 점에 교차한다

그 교차점이 바로 ‘하나의 직선 존재’를 의미

3. 직선 검출을 위한 일반화된 허프 변환 (ρ, θ 표현)

ab 공간으로 변환하면, 위의 (y=ax+b) 표현은 수직선(vertical line) 을 표현할 수 없다는 한계가 있다.

xy 공간에서의 직선이 y축과 평행한 수직선이라면 기울기 a가 ∞이고 y 절편은 b이기 때문에 ab 공간에서 교점이 (∞, b)가 되는데 이는 ab 공간에서 표현할 수 없다.

그래서 실제 허프 변환에서는 아래와 같이 변환합니다:

\(\rho = x \cos\theta + y \sin\theta\)

( \rho ): 원점에서 직선까지의 거리
( \theta ): 직선의 법선(normal) 방향과 x축이 이루는 각도

→ 이 식은 모든 직선을 (ρ, θ) 로 유일하게 표현할 수 있게 해줍니다.

그러면 이제 직선의 방정식을 xy 공간에서 ρ와 θ의 공간으로 변환할 수 있음.

변환했을 때 직선이 아닌 곡선으로 표현되는 것만 제외하면 원리는 ab공간으로 변환했을 때와 같다.

xy 공간에서의 점들을 ρ와 θ의 공간으로 변환했을 때 만들어지는 곡선들이, 많이 교차되는 점을 축적 배열로 찾아 직선을 검출하게 된다.

“영상 공간의 점들이 파라미터 공간에서는 곡선을 만든다.
여러 곡선이 교차하는 곳이 곧 ‘하나의 형태(직선, 원)’의 존재를 의미한다.”

즉, 픽셀 단위로 직선을 찾지 않고,
모든 가능한 직선 후보에 ‘투표’하고, 투표가 몰린 곳이 진짜 직선인 곳.

4. 알고리즘 동작 과정 (직선 검출)

Step 1. Edge Detection

Canny, Sobel 등으로 에지(윤곽선) 픽셀만 추출.

Step 2. Parameter Voting (투표 과정)

각 에지 픽셀 (x, y)에 대해 가능한 모든 각도 θ(예: -90° ~ 90°)에 대해
\( \rho = x \cos\theta + y \sin\theta \)
를 계산.
(ρ, θ) 값을 누적기(accumulator) 공간에 “투표(vote)” 함.
- 예: accumulator[ρ, θ]++
- 같은 직선 위의 픽셀들은 동일한 (ρ, θ)에 투표하게 됨.

Step 3. Peak Detection

누적 공간에서 가장 많이 투표된 (ρ, θ) 값을 찾음 → 그게 곧 “직선 존재”.

Step 4. 직선 복원

찾은 (ρ, θ)를 이용해 원래 영상에 직선을 그립니다:
\(x\cos\theta + y\sin\theta = \rho\)

6. 허프 변환의 응용 확장

직선(Line)	( \rho = x\cos\theta + y\sin\theta )	2D 누적공간 (ρ,θ)
원(Circle)	( (x - a)^2 + (y - b)^2 = r^2 )	3D 누적공간 (a,b,r)
타원(Ellipse)	복잡한 파라미터식 (5D)	일반화된 허프 변환
임의곡선(Generalized Hough)	룩업 테이블 기반	패턴 매칭 기반

7. 장점과 한계

✔️ 노이즈에 강함 (투표 기반이므로 일부 손실 무시 가능)	❌ 계산량 많음 (θ,ρ 전 범위 탐색)
✔️ 여러 직선/원 동시 검출 가능	❌ 누적공간 크기 커짐 → 메모리 부담
✔️ 에지가 불완전해도 형태 검출 가능	❌ 파라미터 정밀도(해상도)에 따라 결과 품질 달라짐

Reference

https://developer-lionhong.tistory.com/28#google_vignette

https://janghan-kor.tistory.com/701

https://sunny-archive.tistory.com/93
https://kys0411.tistory.com/120

https://velog.io/@jungizz_/%EC%98%81%EC%83%81%EC%B2%98%EB%A6%AC-5.-Image-Restoration

'AI > Computer Vision' 카테고리의 다른 글

[CV] BN, Batch Nomarlization 설명, CNN+BN 역할 (0)	2025.10.23
[CV] FFT란 Fast Fourier Transform (0)	2025.10.16
[CV] Image degradation 직접 구현 -① (Blur, Periodic Noise, Low Contrast) (0)	2025.10.14
[CV] Diagonal Gaussian Distribution 설명 (0)	2025.09.29
[CV] Watermark 논문 정리 모음 (0)	2025.09.24

현재글[CV] Image Processing 개념 총정리! / Image degradation 직접 구현 -②③ (Blur, Periodic Noise, Low Contrast)

프로그래밍선

귀여운 뽀뿌 🐶💗🤍

경사하강법, depth pro, PIP, error, cv2, 프로그래머스, LLM, diffusion, tmpi, tiled multiplane images for practical 3d photography, streamlit, Python, 챗봇만들기, novel view synthesis, nvs, depth, 논문리뷰, Computer Vision, SGD, Depth estimation,

Today :
Yesterday :

« 2026/02 »
일	월	화	수	목	금	토
1	2	3	4	5	6	7
8	9	10	11	12	13	14
15	16	17	18	19	20	21
22	23	24	25	26	27	28