🏛️ RNN(순환 신경망) 요약 정리
1. RNN의 도입 배경: 메모리의 필요성
먼저 기존 신경망과 구별되는 RNN의 핵심적인 필요성:
- 가변 길이(Variable Sequence Length):입력 데이터의 길이가 고정되어 있지 않고 변하는 경우를 처리해야 합니다.
- 시간적 의존성(Temporal Dependencies):데이터의 순서와 시간의 흐름에 따른 문맥을 모델링해야 합니다.
- 메모리(Memory)의 도입:RNN은 바로 이 지점에서 '기억(Memory)'이라는 개념을 아키텍처에 도입하여, 이전 단계의 정보를 현재 단계로 전달합니다
2. 5가지 핵심 입력-출력 아키텍처 (Five Primal Architectures)
입력과 출력의 형태에 따라 모델을 5가지 범주로 분류하여 설명하였습니다.
One-to-One (일대일)
- 설명:가장 기본적인 형태의 피드포워드(Feed-forward) 신경망입니다.
- 예시:단일 이미지를 입력받아 단일 클래스로 분류하는 일반적인 이미지 분류(Image Classification)작업.
One-to-Many (일대다)
- 설명:하나의 입력을 받아 시퀀스(연속된) 출력을 생성합니다.
- 예시:이미지 캡셔닝(Image Captioning). 이미지 한 장을 입력하면 문장(단어들의 시퀀스)을 출력합니다.
Many-to-One (다대일)
- 설명:시퀀스 입력을 받아 하나의 출력을 생성합니다.
- 예시:비디오 분류(Video Classification). 비디오 프레임들의 시퀀스를 보고 전체 비디오의 주제(레이블)를 하나로 분류합니다.
Many-to-Many (다대다) - 비동기형 (Sequence-to-Sequence)
- 설명:입력 시퀀스와 출력 시퀀스의 길이가 다르며 정렬되지 않은 경우입니다. 인코더(Encoder)가 입력을 처리하고 디코더(Decoder)가 출력을 생성하는 구조입니다.
- 예시:기계 번역(Machine Translation). 입력된 언어의 단어 순서와 번역된 언어의 단어 순서 및 길이가 다를 때 사용됩니다.
Many-to-Many (다대다) - 동기형 (Synced)
- 설명:입력과 출력 시퀀스가 시간적으로 동기화(Aligned)되어 있는 경우입니다.
- 예시:프레임별 비디오 분류(Per-frame Classification). 비디오의 매 프레임마다 레이블을 지정합니다.
3. RNN의 작동 원리: 내부 상태와 파라미터 공유
RNN을 정의하는 핵심 아이디어는 **내부 상태(Internal State)**의 유지와 갱신입니다.
은닉 상태 (Hidden State, ht):시퀀스가 처리됨에 따라 계속 업데이트되는 내부의 기억입니다.
점화식 (Recurrence Formula):수학적으로 현재의 은닉 상태 ht는 이전 상태 $h_{t-1}$와 현재 입력 xt에 대한 함수로 정의됩니다.
ht=fW(ht−1,xt)
파라미터 공유 (Parameter Sharing):가장 중요한 특징입니다. 동일한 함수 f와 동일한 가중치 파라미터 W가 모든 시간 단계(Time Step)에서 재사용됩니다. 이를 통해 모델은 시퀀스의 길이에 상관없이 작동하며, 시퀀스 내의 위치와 무관하게 패턴을 일반화할 수 있습니다.

바닐라 RNN (Vanilla RNN)의 수식
은닉 상태 계산:
ht=tanh(Whhht−1+Wxhxt)
(이전 상태와 현재 입력의 선형 결합 후 하이퍼볼릭 탄젠트 적용)
출력 계산:
yt=Whyht
(현재 은닉 상태를 선형 투영)
초기 상태 (h0):보통 0으로 설정하거나 학습 가능한 파라미터로 설정합니다.

3. RNN의 작동 원리: 내부 상태와 파라미터 공유
RNN의 핵심은 **내부 상태(Internal State, $h_t$)**를 유지하고 갱신하는 것입니다.
- 점화식 (Recurrence Formula): 현재의 은닉 상태 $h_t$는 이전 상태 $h_{t-1}$와 현재 입력 $x_t$를 사용하여 계산됩니다.
-
$$h_t = f_W(h_{t-1}, x_t)$$
- 파라미터 공유 (Parameter Sharing): 가장 중요한 특징으로, 모든 시간 단계(Time Step)에서 동일한 가중치 파라미터 $W$를 재사용합니다. 이를 통해 시퀀스 길이에 상관없이 모델을 적용할 수 있습니다.
Vanilla RNN의 수식
- 이전 상태와 현재 입력을 선형 결합한 후, 비선형 활성화 함수인 tanh를 통과시켜 현재 상태를 갱신합니다.
4. 시퀀스 처리 및 손실 계산 (Unrolling & Loss)
Unrolling (펼치기):시간 순서에 따른 재귀적 관계를 풀어서 표현하면, 전체 계산 그래프(Computational Graph)를 만들 수 있습니다. 이를 통해 순차적인 의존성이 명확해집니다.
손실(Loss) 계산:Many-to-Many 작업의 경우, 각 시간 단계별로 출력(yt)이 나오고 각각의 손실(Lt)이 발생합니다. 전체 손실은 개별 단계 손실의 합으로 계산됩니다.
5. 예시: 문자 단위 언어 모델 (Character-level Language Model)
교수님은 'hello'라는 단어를 예시로 들어 모델의 학습과 추론 과정을 설명하셨습니다.
학습 과정:
입력 'h' →목표 'e'
입력 'e' →목표 'l'
입력 'l' →목표 'l'
입력 'l' →목표 'o'
테스트(생성) 과정 (Test Time):
첫 입력(예: 'h')을 넣고 점수(Score)를 계산합니다.
Softmax를 통과시켜 다음 문자에 대한 확률 분포를 얻습니다.
이 분포에서 다음 문자를 샘플링합니다.
Autoregressive (자기 회귀):샘플링된 문자를 다음 단계의 입력으로 다시 사용합니다. 이 과정을 반복하여 일관된 텍스트 시퀀스를 생성합니다.
6. 입력의 표현: 임베딩 (Embedding)
입력 데이터를 처리하는 효율적인 방법에 대한 설명이 이어졌습니다.
One-hot Vector의 비효율성:입력 단어나 문자를 One-hot 벡터로 표현하여 가중치 행렬(Wxh)과 곱하는 것은, 실제로는 행렬의 특정 열(Column)을 추출하는 것과 같습니다.
임베딩 레이어 (Embedding Layer):굳이 큰 행렬 곱셈을 수행하는 대신, 인덱스를 사용하여 해당 벡터를 바로 참조(Lookup)하는 방식을 사용합니다.
이는 이산적인(Discrete) One-hot 입력을 밀집된(Dense) 연속 벡터 공간으로 매핑하는 과정입니다.
단어 수준(Word Level)과 같이 카테고리가 매우 많은 경우 계산 효율성을 위해 필수적입니다.
7. 역전파: BPTT (Backpropagation Through Time)
마지막으로 학습을 위한 기울기 계산 방법이 언급되었습니다.
Forward Pass:전체 시퀀스에 대해 출력을 계산하고 손실(Loss)을 구합니다.
Backward Pass:시간 역순으로 그래디언트를 전파합니다.
BPTT:현재 시간(t)의 그래디언트는 과거의 모든 시간 단계로 거슬러 올라가며 전파되어야 합니다. 이는 계산 그래프를 시간 순서대로 펼친 상태에서 역전파를 수행하는 것과 같습니다.
🏛️ RNN 학습과 한계
1. 학습의 효율화: Truncated BPTT
기본적으로 RNN은 모든 시간 단계(Time Step)에 대해 가중치를 공유하므로, 전체 그라디언트는 각 개별 시간 단계에서 계산된 그라디언트의 합으로 계산됩니다. 이를 **BPTT (Backpropagation Through Time)**라고 합니다.
문제점:시퀀스가 매우 길어질 경우, 처음부터 끝까지 Forward/Backward 패스를 수행하는 것은 계산 비용과 메모리 소모가 엄청납니다.
해결책: Truncated BPTT (절단된 BPTT)
전체 시퀀스를 한 번에 학습하는 대신, 작은 덩어리(Sub-sequence)로 나눕니다.
- Forward Pass:은닉 상태(Hidden State)는 시간의 흐름에 따라 계속 전달하여 메모리를 유지합니다.
- Backward Pass:그라디언트 전파는 현재 처리 중인 덩어리 내에서만 수행하고, 일정 단계 이전으로는 끊어버립니다(Truncate).
- 효과:계산 부담과 메모리 사용량을 줄이면서도, 단기 및 중기 정도의 의존성(Dependency)은 학습할 수 있게 됩니다.
2. 응용 사례: 이미지 캡셔닝 (Image Captioning)
RNN의 "One-to-Many" 아키텍처를 활용한 가장 대표적인 컴퓨터 비전 응용 분야입니다. 입력된 이미지를 설명하는 문장(단어 시퀀스)을 생성합니다.
2.1 아키텍처: CNN + RNN
인코더 (Encoder) - CNN:
입력 이미지를 처리하여 **Visual Feature Vector (시각적 특징 벡터, $v$)**라는 압축된 표현으로 변환합니다. (일반적으로 FC 레이어 직전의 값을 사용)
디코더 (Decoder) - RNN:
벡터 $v$를 입력받아 단어 시퀀스를 하나씩 생성합니다.
2.2 동작 과정 (Forward Pass)
초기화:
가장 간단한 구현에서는 $v$를 RNN의 초기 은닉 상태($h_0$)를 초기화하는 데 사용합니다.
첫 입력($x_0$)으로는 특별한 <START>토큰을 넣어줍니다.
생성 루프:
모델이 첫 단어($y_1$)를 예측합니다.
이 예측된 단어(또는 정답 단어)를 다음 시간 단계의 입력($x_1$)으로 다시 넣어줍니다 (Autoregressive).
종료:
모델이 <END>토큰을 출력할 때까지 이 과정을 반복합니다.
2.3 개선된 입력 방식 (Attention의 전조)
단순히 초기 상태($h_0$)에만 $v$를 넣는 것이 아니라, 모든 시간 단계의 입력에 $v$를 포함시키는 방식이 더 좋은 성능을 냅니다.
수식 변화:
$$h_t = f(h_{t-1}, x_t, \mathbf{v})$$
이렇게 하면 캡션을 생성하는 내내 모델이 이미지를 '참조'할 수 있게 됩니다.
3. RNN의 치명적 문제: 기울기 소실과 폭발 (Vanishing & Exploding Gradient)
RNN 학습 시 발생하는 가장 큰 실질적인 문제로, 장기 의존성(Long-term dependency)학습의 어려움을 지적하셨습니다.
이는 역전파 과정에서의 반복적인 행렬 곱셈때문입니다.
3.1 수학적 원인 분석
역전파(Backpropagation) 시, 시간 $t$에서의 에러를 과거 $k$시점까지 전파하려면 연쇄 법칙(Chain Rule)에 의해 다음과 같은 형태의 미분값을 곱해 나가야 합니다.
$$\frac{\partial h_t}{\partial h_{t-k}} = \prod_{i=t-k+1}^{t} \frac{\partial h_i}{\partial h_{i-1}}$$
여기서 $\frac{\partial h_i}{\partial h_{i-1}}$는 **가중치 행렬 $W$**와 활성화 함수(tanh)의 도함수의 곱으로 이루어집니다. 즉, $k$단계만큼 거슬러 올라가면 $W$가 $k$번 곱해지는 효과가 나타납니다 ($W^k$).
3.2 SVD (특이값 분해)를 통한 해석
행렬 $W$의 **특이값(Singular Value)**을 통해 이를 설명하셨습니다.
행렬 $W$는 SVD를 통해 특이값과 특이 벡터로 분해될 수 있습니다.
거듭제곱 $W^k$는 특이값들의 $k$제곱 형태로 동작합니다.
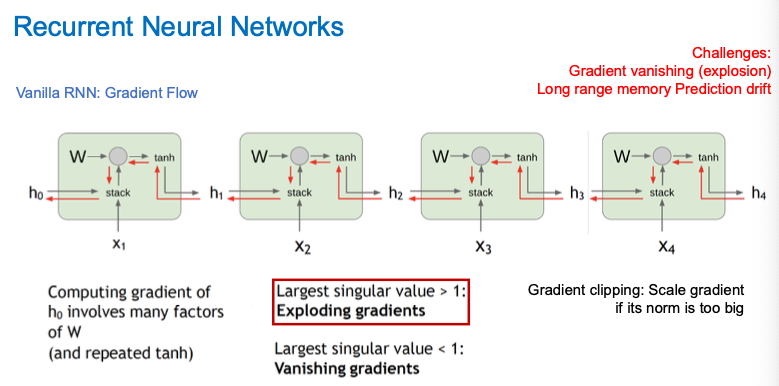
Vanishing Gradient (기울기 소실):
조건:$W$의 가장 큰 특이값(Largest Singular Value)이 1보다 작을 때.
현상:$W$를 계속 곱하면 값은 0에 수렴하게 됩니다.
결과:먼 과거의 정보가 현재에 미치는 영향(Gradient)이 사라져서, 모델이 장기 기억(Long-term Memory)을 잃어버립니다.(예: 문단 맨 앞의 주어를 문단 끝에서 기억하지 못함)
Exploding Gradient (기울기 폭발):
조건:$W$의 가장 큰 특이값이 1보다 클 때.
현상:$W$를 계속 곱하면 값이 무한대로 발산합니다.
결과:학습 과정(Optimization)이 불안정해지고 파라미터가 튀어버립니다.
3.3 활성화 함수의 영향
$\tanh$함수의 도함수는 최댓값이 1입니다(0과 1 사이).
따라서 활성화 함수의 미분값들을 계속 곱하는 과정 자체도 기울기를 작게 만드는(Vanishing) 요인이 됩니다.
RNN의 한계 극복과 심화 아키텍처
1. 기울기 문제의 해결 (Gradient Solutions)
지난 시간에 이어 가중치 행렬 W의 **특이값(Singular Value)**이 미치는 영향에 대한 논의가 마무리되었습니다.
A. 기울기 폭발 (Exploding Gradient)
원인:행렬 W의 가장 큰 특이값이 1보다 클 때, 역전파 과정에서 W가 거듭 곱해지며(Wk) 기울기가 발산합니다.
해결책: Gradient Clipping (그래디언트 클리핑)
이 문제는 비교적 다루기 쉽습니다.
기울기의 Norm(크기)이 특정 임계값(Threshold)을 넘으면, 강제로 값을 줄여서(Scaling) 임계값 안으로 들어오게 자릅니다.
B. 기울기 소실 (Vanishing Gradient)
원인:특이값이 1보다 작을 때 발생하며, 이는 네트워크가 장기 기억을 잃게 만듭니다.
해결책:단순한 테크닉으로는 해결이 어렵고, 근본적인 아키텍처의 변화가 필요합니다. →LSTM의 등장 배경
2. LSTM (Long Short-Term Memory)
LSTM은 긴 시간 동안 정보를 저장하고 접근할 수 있도록 설계되었습니다. 핵심 혁신은 **Cell State(셀 상태)**와 게이트(Gate)구조입니다.
A. 핵심 구조: Cell State (Ct)
개념:Hidden State(ht)와 개념적으로 분리된 별도의 메모리 트랙입니다.
특징:정보가 큰 방해 없이 흘러갈 수 있는 '고속도로'와 같습니다. 이 경로를 통해 정보가 추가되거나 제거됩니다.
B. 3가지 게이트 (Gates)
정보의 흐름은 시그모이드 신경망 레이어와 점곱(pointwise multiplication) 연산으로 구성된 '게이트'에 의해 제어됩니다.
Forget Gate (망각 게이트):
이전 Cell State (Ct−1)에서 버릴 정보를 결정합니다.
Input Gate (입력 게이트):
현재 입력(xt)에서 들어온 새로운 정보 중 Cell State에 저장할 정보를 결정합니다.
Output Gate (출력 게이트):
업데이트된 Cell State (Ct)를 바탕으로, 현재의 Hidden State (ht)로 내보낼 정보를 결정합니다.
C. 기울기 소실을 막는 원리 (Gradient Flow)
덧셈 연산 (Additive Interaction):Vanilla RNN은 매번 행렬 곱셈(W×h)을 반복했지만, LSTM의 Cell State 업데이트는 주로 **덧셈(+)과 요소별 곱셈(Element-wise Multiplication)**으로 이루어집니다.
Gradient Superhighway:역전파 시, 덧셈 연산은 그래디언트를 그대로 통과시키는 특성이 있습니다. 이는 ResNet의 Skip Connection과 유사한 원리로, 그래디언트가 소실되지 않고 먼 과거까지 잘 전달되게 합니다.
3. 기타 RNN 변형 모델들
A. Bidirectional RNN (양방향 RNN)
개념:출력값이 과거의 정보뿐만 아니라 미래의 정보에도 의존할 때 사용합니다.
구조:두 개의 독립적인 RNN을 사용합니다.
- 하나: Forward 방향 (과거 →미래)
- 다른 하나: Backward 방향 (미래 →과거)
출력:두 RNN의 출력을 결합하여 최종 출력을 만듭니다. (전체 문맥 파악에 유리)
B. GRU (Gated Recurrent Unit)
개념:LSTM을 약간 단순화시킨 모델입니다.
특징:LSTM과 유사한 성능을 내면서도 구조가 더 간단하여 연산 효율성이 높습니다. 따라서 현대 딥러닝에서 매우 인기 있는 선택지입니다.
4. Summary
RNN의 유연성:One-to-One, Many-to-Many 등 다양한 시퀀스 문제를 모델링할 수 있는 구조적 유연성을 제공합니다.
Vanilla RNN의 한계:개념적으로는 간단하지만, 기울기 소실(Vanishing Gradient)문제로 인해 학습이 매우 어렵고 성능이 잘 나오지 않습니다.
LSTM/GRU의 표준화:
**Additive Interaction(덧셈 상호작용)**과 **Gating Mechanism(게이트 메커니즘)**을 통해 기울기 흐름을 개선했습니다.
행렬 곱셈 대신 **요소별 곱셈(Element-wise multiplication)**을 활용하여 장기 의존성을 효과적으로 포착합니다.
현재 시퀀스 모델링의 가장 일반적이고 견고한(Robust) 선택입니다.
연구 동향:더 간단하면서도 효과적인 Recurrent 아키텍처를 찾는 것은 여전히 활발한 연구 분야입니다.
'AI > Computer Vision' 카테고리의 다른 글
| [CV] Attention 메커니즘과 Transformer의 기초 (0) | 2026.02.12 |
|---|---|
| [CV] FRR, Anomaly Detection 기본개념, Visually Ambiguous Features 이란 (1) | 2026.01.13 |
| [CV] BN, Batch Nomarlization 설명, CNN+BN 역할 (0) | 2025.10.23 |
| [CV] FFT란 Fast Fourier Transform (0) | 2025.10.16 |
| [CV] Image Processing 개념 총정리! / Image degradation 직접 구현 -②③ (Blur, Periodic Noise, Low Contrast) (0) | 2025.10.16 |