얀 르쿤의 레 제파!
여기서 le: lean - 군더더기없는 이란 뜻이다
GitHub - galilai-group/lejepa
Contribute to galilai-group/lejepa development by creating an account on GitHub.
github.com

목차
1. Introduction (서론)
2. Background on Joint-Embedding Predictive Architectures (JEPA 배경지식)
- 2.1 What is a JEPA? (JEPA란 무엇인가?)
- 2.2 The Need for Reliable Pretraining (신뢰할 수 있는 사전학습의 필요성)
- 2.3 The Need for Actionable Theory (실용적인 이론의 필요성)
3. The Isotropic Gaussian is All You Need for Reliable SSL (신뢰할 수 있는 자기지도학습에 필요한 것은 등방성 가우시안 분포뿐이다)
- 3.1 The Linear Case: Linear Probing (선형 사례: 선형 평가)
- 3.2 The Non-Linear Case: k-NN and Kernel Methods (비선형 사례: k-NN과 커널 방법)
- 3.3 Geometric and Practical Insights (기하학적 및 실용적 통찰)
4. SIGReg: Reliable Isotropic Gaussian Regularization in High-Dimension (SIGReg: 고차원에서의 신뢰할 수 있는 등방성 가우시안 정규화)
- 4.1 Hypothesis Testing as a Judge (심판으로서의 가설 검정)
- 4.2 Candidate Statistical Tests are not Scalable (후보 통계 테스트들은 확장 가능하지 않다)
- 4.2.1 Moments are Unstable (모멘트(순간)는 불안정하다)
- 4.2.2 Cumulative Density Functions are Impractical (누적분포함수는 비실용적이다)
- 4.2.3 Characteristic Functions are Scalable (특성함수는 확장 가능하다)
- 4.3 How SIGReg Beats the Curse of Dimensionality (SIGReg는 어떻게 고차원의 저주를 이겨내는가)
5. LeJEPA: Stable and Scalable Implementation (LeJEPA: 안정적이고 확장 가능한 구현)
- 5.1 LeJEPA: SIGReg + Prediction Loss (LeJEPA: SIGReg + 예측 손실)
- 5.2 Relation to Prior Work (이전 연구와의 관계)
6. LeJEPA: Empirical Validation (LeJEPA: 경험적 검증)
- 6.1 LeJEPA is Stable and Reliable (LeJEPA는 안정적이고 신뢰할 수 있다)
- 6.2 LeJEPA’s Training Loss is a Reliable Indicator of Downstream Performance (LeJEPA의 학습 손실은 최종 성능의 신뢰할 수 있는 지표이다)
- 6.3 In-Domain Pre-training Beats Frontier Models Transfer (특정 분야 사전학습이 범용 모델 전이학습을 이긴다)
- 6.4 LeJEPA Scales Across Data and Models (LeJEPA는 데이터와 모델에 걸쳐 확장된다)
- 6.5 Emergent Semantic Structure in LeJEPA Representations (LeJEPA 표현에서 창발하는 의미론적 구조)
7. Conclusion (결론)
들어가기 전, LeJEPA의 철학: 근본으로 돌아가는 용기
LeJEPA는 단순한 '새로운 알고리즘'이 아니라, AI 연구를 어떻게 해야 하는가에 대한 하나의 강력한 선언문이자 패러다임 전환을 요구하는 외침입니다.
근본으로 돌아가는 용기 (The Courage to Return to First Principles)
이 철학은 다음과 같은 네 가지 핵심 기둥으로 이루어져 있습니다.
1. 이론 우선주의: '어떻게'보다 '왜'를 먼저 묻는다 (First Principles over Empiricism)
* 기존의 철학 (Ad-hoc R&D):
모델이 자꾸 붕괴하네. 어떻게 해결하지? Teacher-Student 구조를 넣어볼까? Stop-Gradient를 써볼까?"
→ **문제가 터지면 임시방편(heuristic)으로 땜질하는 방식.
* LeJEPA의 철학:
"잠깐. '표현 붕괴'가 없는 이상적인 상태란 무엇인가? 어떤 분포가 최적의 표현을 보장하는가? 왜 그 분포여야만 하는가?"
→ 가장 근본적인 질문("Why?")에서 출발하여, 그에 대한 이론적인 답("Isotropic Gaussian")을 먼저 찾고, 그 답을 구현할 최선의 방법("How?", SIGReg)을 설계하는 방식.
이것은 다리를 지을 때, 무작정 나무판자를 여러 개 덧대보는 것이 아니라, 먼저 물리학의 원리를 이해하고 완벽한 아치 구조를 설계하는 것과 같습니다. LeJEPA는 AI 연구가 더 이상 '어두운 방에서 코끼리 만지기'식의 경험주의에만 의존해서는 안 되며, 수학과 이론이라는 단단한 지반 위에 서야 한다고 주장합니다.
2. 미니멀리즘: 복잡함은 무지의 증거다 (Simplicity as a Virtue)
* 기존의 철학 (Ad-hoc R&D):
복잡한 Teacher-Student 구조, 여러 개의 하이퍼파라미터, 복잡한 스케줄러 등은 모델을 강력하게 만드는 '필수적인 부품'이라고 여겨졌습니다.
* LeJEPA의 철학:
그 모든 복잡함은 우리가 문제의 근본 원인을 몰랐기 때문에 추가된 **'군더더기(fat)'** 일 뿐이라고 선언합니다. 문제의 본질(분포 최적화)을 정확히 이해하고 나면, 그 모든 장치들은 필요 없어지며, 오히려 극도로 **단순하고(lean), 우아한(elegant)** 해결책이 드러난다는 것입니다.
이것은 어수선하게 물건이 널려있는 방을 정리하는 것과 같습니다. 진짜 중요한 것이 무엇인지 깨닫고 나면, 대부분의 잡동사니를 버리고도 훨씬 더 효율적이고 아름다운 공간을 만들 수 있습니다. LeJEPA에게 '단순함'은 타협이 아니라, 깊은 이해를 통해 도달할 수 있는 궁극적인 미덕입니다.
3. 해방: 보편성은 자유를 낳는다 (Generality as Freedom)
* 기존의 철학 (Ad-hoc R&D):
최신 자기지도학습 방법론들은 대부분 ViT라는 특정 아키텍처에 맞춰 설계되었습니다.
이는 연구자들을 ViT라는 '울타리' 안에 가두는 결과를 낳았습니다.
* LeJEPA의 철학:
자신들의 방법론이 '분포'라는 수학적 개념에 기반하기 때문에, 그 분포를 만들어내는 아키텍처가 ViT이든, ResNet이든, ConvNeXt이든 상관없이 작동해야 한다고 믿습니다. 그리고 실제로 그것을 증명해 보입니다.
이것은 특정 자물쇠만 열 수 있는 '전용 열쇠'가 아니라, 세상의 모든 자물쇠를 열 수 있는 '마스터 키'를 만드는 것과 같습니다. LeJEPA는 연구자들을 특정 아키텍처의 종속에서 **'해방'** 시켜, 자신의 문제와 자원에 맞는 어떤 모델이든 자유롭게 선택할 수 있는 **'자유'** 를 주고자 합니다.
4. 신뢰: 과정은 투명해야 한다 (Transparency and Trust)
* 기존의 철학 (Ad-hoc R&D):
학습 손실 곡선과 최종 성능이 따로 노는 경우가 많았습니다.
연구자들은 "학습이 잘 되고 있는지" 알기 위해, 비싼 평가를 계속 돌려보는 '깜깜이 비행'을 해야 했습니다.
* LeJEPA의 철학:
잘 설계된 학습 과정이라면, 그 과정 자체가 정직한 '신호'를 보내야 한다고 믿습니다. LeJEPA의 학습 손실은 최종 성능과 99%에 가까운 상관관계를 보입니다.
이는 '성적표는 정직해야 한다'는 철학과 같습니다. 학생이 열심히 공부하면(손실이 낮아지면), 성적이 오르는 것(성능이 높아지는 것)이 당연해야 합니다. LeJEPA는 개발자에게 **"과정을 믿으세요. 손실이 떨어지고 있다면, 당신은 올바른 길을 가고 있는 것입니다"** 라는 강력한 **'신뢰'** 를 제공합니다.
결론적으로 LeJEPA는 "더 이상 복잡한 트릭의 시대는 끝났다. 이제는 증명 가능하고, 단순하며, 보편적인 원칙에 기반한 AI 연구의 시대로 나아가야 한다" 는 강력한 철학적 메시지를 던지고 있습니다.
0. Abstract
Learning manipulable representations of the world and its dynamics는 AI의 핵심 과제임.
Joint-Embedding Predictive Architectures (JEPAs)는 유망한 blueprint를 제공하지만, practical guidance와 theory의 부족으로 ad-hoc R&D로 흐르는 문제가 있었음.
본 논문에서는 JEPAs에 대한 comprehensive theory를 제시하고, 이를 LeJEPA라는 lean하고 scalable하며 theoretically grounded된 training objective로 구체화함.
- 첫째, downstream prediction risk를 최소화하기 위해 JEPA의 embedding들이 따라야 하는 최적의 distribution으로 isotropic Gaussian을 식별함.
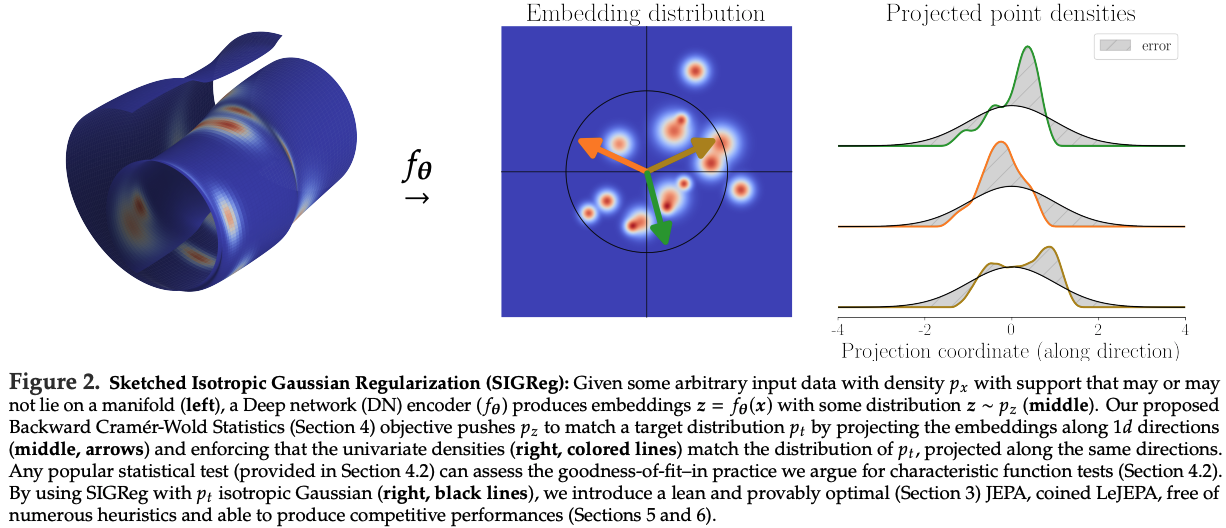
- 둘째, embedding을 그 ideal distribution에 도달하도록 제약하는 새로운 objective인 Sketched Isotropic Gaussian Regularization (SIGReg)를 도입함.
JEPA predictive loss와 SIGReg를 결합함으로써 LeJEPA가 구성되며, 다음과 같은 다양한 theoretical/practical benefit이 제공됨:- (i) 단 하나의 trade-off hyperparameter만 필요함,
- (ii) time/memory complexity가 linear임,
- (iii) hyper-parameter, architecture(ResNets, ViTs, ConvNets), domain 전반에서 stability가 확보됨,
- (iv) heuristics-free임(예: stop-gradient 없음, teacher–student 없음, hyper-parameter scheduler 없음),
- (v) distributed training에 friendly한 구현이 가능하며 약 50줄의 코드만 필요함.
Empirical validation은 scale과 domain이 서로 다른 10개 이상의 dataset과 60개 이상의 architecture를 포괄함.
예시로, imagenet-1k로 pretraining을 수행하고 backbone을 frozen한 상태에서 linear evaluation을 수행할 때, LeJEPA는 ViT-H/14에서 79%에 도달함.
본 논문은 LeJEPA가 제공하는 simplicity와 theory-friendly ecosystem이 self-supervised pre-training을 AI 연구의 core pillar로 다시 자리매김시키기를 기대함 (GitHub repo).

1. Introduction
세계와 그 dynamics에 대한 manipulable representation을 학습하는 일은 AI에서 오래된 질문임.
그 뿌리는 수세기 전까지 거슬러 올라감 [Von Helmholtz, 1867, Tolman, 1948, Gregory, 1980, Sutton, 1991, Friston, 2010]. 이미지 인식, 로보틱스, 물리, 우주 탐사 등 다양한 domain 전반에서, 이를 관통하는 질문은 관측(observations)으로부터 organized되고 actionable한 high-dimensional embedding space를 어떻게 학습하느냐임.
관측을 embedding으로 매핑하기 위해 Deep Networks—parameterized nonlinear operator \(f_\theta\)—를 사용하는 것은 그 퍼즐의 표준적인 첫 번째 조각임 [LeCun et al., 2015, Goodfellow et al., 2016].
두 번째 조각은 덜 표준화되어 있으며, \(f_\theta\)를 어떻게 train하느냐임.
Joint-Embedding Predictive Architectures (JEPAs)는 semantically related view들의 embedding들 사이 predictive agreement를 최대화함으로써 \(f_\theta\)를 학습하는 방식을 제안함 [Bromley et al., 1993, LeCun, 2022, Balestriero et al., 2023].
View는 두 형태로 올 수 있음: transformation 또는 corruption임.
masking, cropping, blurring, temporal/spatial translation, geometric/photometric transformation, viewpoint change, 서로 다른 sensor modality에서의 view 등으로 구성될 수 있음.
Supervised 형태의 view는 image-caption pair, text-code pair 등 human-produced component를 포함함 [Tian et al., 2020].
어떤 경우든, view들은 prediction task가 \(f_\theta\)의 embedding을 데이터에 존재하는 underlying knowledge 쪽으로 align할 수 있도록 어느 정도의 semantic relationship을 공유할 것이 기대됨.
하지만 JEPA의 prediction task에는 failure mode가 존재함.
예를 들어 representation collapse가 있으며, 이는 \(f_\theta\)가 모든 입력을 거의 동일한 embedding으로 매핑하는 경우(complete collapse) 또는 low-dimensional subspace로 매핑하는 경우(dimensional collapse)임 [Jing et al., 2021][Jing et al., 2021, Cosentino et al., 2022, Balestriero and LeCun, 2022].
이런 shortcut solution을 완화하기 위해, SOTA recipe들은 heuristics에 의존함—stop-gradient [Chen et al., 2020a], asymmetric view generation [Wang et al., 2022], carefully tuned EMA schedule을 갖는 teacher–student network [Caron et al., 2021, Tian et al., 2021], explicit normalization 및 whitening layer [Ermolov et al., 2021, Chen et al., 2021]—그리고 hyperparameter의 섬세한 균형이 필요함.
brittle은 “잘 깨지는(부서지는)”을 비유로 써서, 조금만 조건이 바뀌어도 성능/학습이 쉽게 망가지거나 불안정해지는 상태를 뜻함.
그 결과, 현재 JEPA training은 brittle해졌고, 대부분의 연구는 theoretical foundation을 거의 탐구하지 않은 채 data scaling [Vo et al., 2024], model scaling [Fan et al., 2025], 심지어 post-training Rodas et al. [2025] 쪽으로 이동함.
본 연구는 JEPAs를 지탱하는 fundamental design principle 일부를 다시 질문함으로써 이 사이클을 끊고자 함.
이러한 introspection은 “JEPAs가 따라야 할 necessary condition은 무엇인가?”를 묻는 것에서 시작됨. 그 minimal condition들은 새로운 lean JEPA를 설계하기 위한 axiom으로 작동함.
- 본 논문은 두 가지 axiom을 식별함:
- (i) prediction task를 해결함과 동시에
- (ii) embedding이 isotropic Gaussian distribution을 따르도록 강제함(Section 3)임.
(i)는 standard practice를 따르는 반면 [Balestriero and LeCun, 2022], (ii)를 강제하기 위해 Section 4에서 새로운 distribution matching objective—Sketched Isotropic Gaussian Regularization (SIGReg)—를 도입함.
SIGReg의 사용은 representation collapse를 막기 위해 이전에 사용되던 수많은 heuristics의 필요를 제거할 뿐 아니라, memory 및 computational complexity가 dimension과 sample size에 대해 linear임에 따라 favorable scaling property도 보임.
결정적으로, SIGReg의 isotropic Gaussian enforcement는 collapsed shortcut solution을 해결하며, post-training 이후 마주칠 downstream task 공간 전체에 대해 모델의 expected risk를 provably 최소화함.
그 결과로 얻어지는 JEPA 해법—Latent-Euclidean JEPA (LeJEPA)로 명명됨—이 Section 5에서 소개됨.
Theoretical optimality를 넘어서, LeJEPA는 (i) provable statistical guarantee, (ii) teacher–student network 같은 heuristics 제거, (iii) linear memory 및 computational complexity, 그리고 가장 중요하게 (iv) dataset/architecture/scale 전반에서 out-of-the-box로 작동하는 단일 trade-off parameter를 갖는 unified design을 제공함(Section 6 참조).
아래에 기여를 요약함.
- Contribution 1:
foundation model을 위한 optimal embedding distribution을 증명함.
Isotropic Gaussian이 광범위한 task family에 걸쳐 downstream prediction risk를 uniquely 최소화함을 정립함.
Section 3에서 linear probe(Section 3.1)와 nonlinear probe(Section 3.2) 모두에 대해 이 결과를 엄밀히 유도하며, (f_\theta)의 embedding이 어떤 distribution을 따라야 하는지에 대한 최초의 principled answer를 제시함.
이 theoretical result는 JEPA design을 heuristic 탐색에서 targeted optimization으로 전환시킴. - Contribution 2:
correctness가 provable하면서 scale에서 computationally efficient한 distribution matching objective인 SIGReg를 도입함. Sketched Isotropic Gaussian Regularization (SIGReg)는 random projection과 characteristic-function matching을 통해 distributional alignment를 강제하는 새로운 objective로 제시됨(Section 4 및 Figure 2). SIGReg는 statistical guarantee를 제공함(Sections 4.1, 4.2)과 동시에 linear complexity와 bounded gradient를 달성하며, 이는 기존 distribution matching method들이 제공하지 못한 조합임. 특히 projection-based construction을 통해 curse of dimensionality를 극복함(Section 4.3)으로써, high-dimensional embedding에 대해 theoretically sound하면서도 practically efficient하도록 만듦. - Contribution 3:
construction 자체로 collapse를 제거하는 statistically optimal JEPA인 LeJEPA를 설계함.
JEPA의 predictive objective와 isotropic Gaussian을 target으로 하는 SIGReg를 결합함으로써, LeJEPA—Latent-Euclidean JEPA(Section 5)—를 도입함. LeJEPA는 단 하나의 hyperparameter만 요구하며, stop-gradient나 teacher–student architecture 없이 representational collapse를 제거하고, hyperparameter tuning 없이 architecture와 dataset 전반으로 transfer됨. 이는 principled theory가 직접적으로 practical simplicity를 산출함을 보여줌. - Contribution 4:
다양한 architecture 전반에서 scale로 LeJEPA를 검증하고, in-domain pretraining이 viable함을 정립함. 실험(Section 6)은 ViT, ConvNeXt, ResNet, MaxViT, Swin Transformer를 포함하며, parameter 수가 10억에 근접하는 scale까지 확장됨. 이 구간에서 LeJEPA는 SOTA method들과 match하거나 이를 초과하면서도 training simplicity와 robustness를 유지함.
또한 domain-specific dataset(Galaxy10, Food101)에서는 target data에서 직접 pretrained했을 때 LeJEPA가 DINOv2 기반 transfer learning을 outperform함. 이는 transfer learning paradigm에 도전하며, principled SSL이 small dataset에서는 impractical하다고 여겨졌던 effective in-domain pretraining을 열 수 있음을 보여줌.
2 Background and Notations
본 절에서는 본 manuscript 전반에서 사용할 notation을 먼저 소개함(Section 2.1).
이후 JEPAs를 리뷰함(Section 2.2).
마지막으로 JEPA design을 연구한 기존 문헌을 정리함(Section 2.3).
2.1 Notations and Definitions
Data.
형태가 \((N, V, D) \in \mathbb{N}^{*3}\) 인 dataset을 보유하고 있다고 가정함.
여기서 N은 sample 개수, V는 view 개수, D는 dimension을 의미함. Dataset의 한 entry는 다음과 같이 접근됨.
\(xn,v,d\mathbf{x}_{n,v,d}\)
이 차원들은 보통 다음처럼 해석됨.
- N은 서로 독립인 sample의 개수임(예: 서로 다른 image 또는 서로 다른 video).
- V는 view의 개수임(예: image에 대한 data-augmentation들, video에 대한 frame들).
- D는 각 (\mathbf{x}_{n,v})의 dimension임(예: image의 RGB pixel 개수).
많은 경우 V에 대한 ordering은 time으로 주어짐.
하지만 어떤 경우에는 ordering이 무의미해짐(예: 하나의 image에 대한 data-augmentation들).
본 연구는 dataset을 \((N, V, D)\) tensor로 조직하는 특정한 선택을 요구하지 않음. 또한 본 논문의 theory와 implementation 어느 쪽도 해당 tensor에 대한 특정 design decision을 가정하지 않음.
다만, 다음 두 가지 성질에는 의존함
- (1) (independence) sample (\mathbf{x}n) 과 (\mathbf{x}{n'}) 는 서로 독립적으로 얻어졌다고 가정됨.
즉,
∀n≠n′, xn and xn′ are independent\(forall n \neq n',\ \mathbf{x}_n \ \text{and}\ \mathbf{x}_{n'}\ \text{are independent}\) - (2) (identically distributed) 모든 \(\mathbf{x}_n\) 에 대해 sampling process가 동일하다고 가정됨. 즉,
∀n, xn are identically distributed\(forall n,\ \mathbf{x}_n \ \text{are identically distributed}\)
Deep Networks.
오늘날 AI solution은 Deep (Neural) Networks(DNs)에 의존함. DNs는 많은 수의 parameterized linear/nonlinear operator의 composition으로 구성됨. DN의 mapping을 다음처럼 표기함.
\(fθ:RD→RKf_\theta : \mathbb{R}^D \rightarrow \mathbb{R}^K)
여기서 K는 embedding space의 dimension임. \(f_\theta\)의 내부 구조(internals)는 연구자가 데이터에 대한 prior knowledge를 최대한 반영하도록 설계함. 본 연구에서 \(f_\theta\)의 구체적 details는 중요하지 않음. 제안하는 LeJEPA가 어떤 \(f_\theta\)에도 out-of-the-box로 작동함을 이후에 보이기 때문임.
어쨌든 learnable parameter는 모두 벡터 \(\theta \in \mathbb{R}^P\) 에 모아짐. 여기서 P는 전체 parameter 개수임. AI 연구의 핵심 과제는 올바른 architecture와 training objective를 설계하여, gradient descent로 \(\theta\)가 학습되도록 만들고, 궁극적으로 유용한 system 혹은 foundation model \(f_\theta\)를 생산하도록 하는 것임.
JEPAs.
Foundation model은 내부 parameter \(\theta\)를 전혀 바꾸지 않고도 수많은 downstream task를 풀 수 있는 system(예: DN)이라 정의됨.
이는 training task만을 고려하는 supervised model과는 뚜렷이 대비됨.
JEPAs는 foundation model을 만들기 위한 vehicle로서 LeCun [2022]에 의해 공식적으로 소개됨.
JEPA의 core building block은 siamese network [Bromley et al., 1993], predictive coding [Helmholtz et al., 1867, Bruner and Postman, 1949] 등 well-established technique들에 기반함.
JEPAs의 정확한 blueprint는 use-case마다 크게 달라지지만, 모두 두 가지 핵심 원리에 의존함.
- (i) 한 view (\mathbf{x}{n,v})의 embedding을 다른 view (\mathbf{x}{n,v'})의 embedding으로부터 예측할 수 있어야 하며((v' \neq v)), 동시에
- (ii) embedding이 degenerate해지지 않도록 보장해야 함.
구체적으로, JEPA가 설계되고 학습되면 zero-shot 혹은 few-shot으로 다양한 downstream task를 풀 수 있어야 함.
JEPA objective function과 (\mathbf{x})에 대한 몇 가지 example은 Equation (1)에 제시됨.
Predictability criterion은 partial view들의 embedding (Enc(\mathbf{x}{n,v,.}))와 (Enc(\mathbf{x}{n,v',.}))를 어떤 metric(예: (\ell_p))으로 직접 비교하는 방식으로 수행될 수 있음. 어떤 경우에는 Pred라고 명명된 추가 DN을 사용하여,
Pred(Enc(xn,v,.)) vs. Enc(xn,v′,.)Pred(Enc(\mathbf{x}_{n,v,.})) \ \text{vs.}\ Enc(\mathbf{x}_{n,v',.})
를 비교하기도 함. 이는 서로 다른 view들이 갖는 information content에 asymmetry가 존재할 때만 정당화됨. 예를 들어 robotics data에서 observed action에 조건부로 prediction을 하도록 하는 경우가 해당됨 [Khazatsky et al., 2024].
2.2 The Need for Reliable Pretraining
JEPA의 prediction task는 데이터에 대한 a priori knowledge를 바탕으로 설계됨.
\(\mathbf{x}\)를 구성하여 view들이 우리가 포착하고자 하는 relevant information content를 공유하게 만드는 일은 비교적 직관적이므로, prediction task의 설계는 종종 자연스럽게 이루어짐.
반면 “anti-collapse” criterion의 설계는 Whac-A-Mole 게임에 훨씬 더 가까움.
오늘날의 설계는 degenerate shortcut solution이 training 중에 발생하지 않기를 기대하며, under-specified safeguard들을 다양하게 섞어 사용하는 방식에 의존함.
이런 메커니즘에는 (i) feature whitening [Ermolov et al., 2021, Bardes et al., 2021], (ii) negative sample [Chen et al., 2020a, He et al., 2020], (iii) stop-gradient를 포함하는 asymmetric view 및 teacher-student network [Caron et al., 2021, Assran et al., 2023] 등이 포함됨.
이 메커니즘들은 적어도 다음 한계 중 두 가지 이상을 가짐.
- (i) under-specification, 즉 embedding이 degenerate configuration에 있어도 criterion이 최소화될 수 있음,
- (ii) mini-batch size 및/또는 embedding dimension에 대해 time/memory complexity가 quadratic임,
- (iii) data distribution, hyperparameter, architecture에 대한 sensitivity가 큼,
- (iv) theoretical understanding 및 guarantee가 부족함.
2.3 The Need for Actionable Theory
수십 년 동안 AI의 두 가지 주요 해법은 supervised learning [LeCun et al., 2015]과 reconstruction을 통한 learning [Rumelhart et al., 1986]이었음. 때로는 semi-supervised learning처럼 둘을 결합하기도 함 [Kingma et al., 2014]. Supervised learning에서는 label이 semantically similar sample들이 embedding space에서 서로 가깝도록 보장하는 동시에, complete representation collapse를 방지함. 특히 supervised learning에서는 class 개수의 함수로 collapse의 정도를 측정하는 것이 가능함 [Papyan et al., 2020].
Reconstruction objective 역시 representation collapse를 막는 데 적합함. 원본 input이 embedding으로부터 복원되어야 하므로, embedding은 input에 대해 가능한 한 informative해야 함. 다만 사용자가 training의 일부로 optional denoising task를 설정하는 경우는 예외적으로 허용됨 [Vincent et al., 2010].
Supervised learning과 reconstruction-based learning은 수십 년간 널리 연구되어 왔으므로, practical design을 설명하고 안내하는 방대한 연구가 존재함. 또한 foundation model을 만드는 데 있어서 이들의 한계도 연구되어 왔음 [Balestriero and LeCun, 2024, Van Assel et al., 2025].
하지만 더 최근의 JEPAs는 그렇지 않음. Empirical advance가 빠르게 누적되어, 내부 동작을 깊이 파고들려는 시도를 앞질러 버리는 상황이 발생함. 이 dynamic은 커뮤니티가 이미 찾아낸 해법에 대한 post-hoc theoretical justification에 집중하도록 만들었음 [Liu et al., 2021, Shwartz Zivand LeCun, 2024, Shwartz-Ziv et al., 2022, Zhang et al., 2023].
대부분의 경우 이러한 연구들은 Mutual Information(MI) [Shannon, 1948, Cover, 1999]를 다루며, 다양한 bound를 통해 기존 method들이 다시 도출됨 [Gutmann and Hyvärinen, 2010, Ma and Collins, 2018, Oord et al., 2018, Poole et al., 2019, Hjelm et al., 2018, McAllester and Stratos, 2020].
기존 연구는 이미 개발된 JEPA를 설명하고 해석하는 데 집중하므로, principled guidance와 innovation이 충분히 제시되지 못했음.
대신 최근의 empirical advance는 더 큰 dataset을 수집하거나, 기존 training recipe를 scale-up하거나 [Goyal et al., 2019, Chen et al., 2020b, Oquab et al., 2023, Fan et al., 2025], 새로운 data curation process를 도출하는 형태로 나타남 [Vo et al., 2024, Kerdreux et al., 2025].
이에 반해, 본 논문의 목표는 이후 Section 3~5에서 first principle로부터 새로운 JEPA solution을 도출하는 것임.
즉, optimality를 위한 proved necessary condition에 기반하여 design을 구성하고, exploratory research, scalability, 그리고 state-of-the-art performance를 finally reconcile할 수 있는 pretraining recipe를 제시하는 것임.

3 Latent Euclidean: Embeddings
Should be Isotropic Gaussian
본 절에서는 근본 질문을 다룸: 어떤 downstream task에 대해서도 empirical risk를 최소화하려면 (Enc(\mathbf{x}))는 어떤 distribution을 따라야 하는가임.
Linear probing(Section 3.1)과 nonlinear probing(Section 3.2) 모두에서 isotropic Gaussian이 유일한(optimal) distribution임을 증명함.
Geometric intuition은 Section 3.3에서 제공됨.
이 theoretical result는 본 논문 JEPA의 필수 design principle을 정립함.
이어서 Section 4에서 이를 달성하기 위한 practical implementation을 제시함.
3.1 Linear Probing
Frozen encoder evaluation에서 가장 널리 쓰이는 방법 중 하나인 linear probe를 분석하여 \(f_\theta\) embedding의 optimal distribution을 먼저 식별함.
구체적으로 다음을 묻는 것임: 임의의 downstream task, 즉 target \(\mathbf{y}\)의 어떤 realization에 대해서도 유리하도록 \(f_\theta(\mathbf{x})\)는 어떤 distribution을 가져야 하는가임.
\(f_\theta(\mathbf{x}_n)\)에서 나온 (N)개의 embedding(각각 (K)-dim)을 모은 행렬을 \(\mathbf{Z} \in \mathbb{R}^{N \times K}\)로 둠. 대응하는 unknown label은 \(\mathbf{y} \in \mathbb{R}^{N}\)로 둠.
일반성을 잃지 않고(univariate target) \(\mathbf{y}\)가 scalar target인 경우를 고려함.
아래 분석은 multivariate target으로도 확장됨.
Linear probe는 다음 least square problem을 최소화함 [Bishop and Nasrabadi, 2006].
\(β^=argminβ∈RK ∥y−Zβ∥22+λ∥β∥22(OLS)\hat{\beta} = \arg\min_{\beta \in \mathbb{R}^{K}} \ \|\mathbf{y}-\mathbf{Z}\beta\|_2^2 + \lambda\|\beta\|_2^2 \qquad (\text{OLS})\)
여기서 \(\hat{\beta}\)는 optimal probe parameter이고, \(\lambda \ge 0\)는 Tikhonov regularizer의 strength를 조절하는 hyperparameter임 [Bishop, 1995, Golub et al., 1999].
\(\mathbf{y}\)를 모르더라도, 추정량 (\hat{\beta})의 bias와 variance를 \(\mathbf{Z}\)의 distribution의 함수로 기술하는 것은 가능함. 동일한 column span을 가지는 두 embedding을 \(\mathbf{Z}{\text{aniso}}, \mathbf{Z}{\text{iso}})\)로 고려함. \(\mathbf{Z}{\text{aniso}}\)의 covariance matrix eigenvalue는 \({\lambda_k}{k=1}^{K}\)로 주어지며, 최소 두 개 이상의 distinct value를 가짐. 반면 \(\mathbf{Z}_{\text{iso}}\)의 covariance matrix eigenvalue는 모두 다음 값으로 동일함.
\(1K∑k=1Kλk\frac{1}{K}\sum_{k=1}^{K}\lambda_k)
따라서 두 candidate embedding \(\mathbf{Z}{\text{aniso}}, \mathbf{Z}{\text{iso}}\)는 동일한 intrinsic feature를 포착하고 동일한 energy를 가지지만, geometry는 서로 다름.
위의 lemma 1과 2로부터 feature distribution은 isotropic이어야 함을 얻음. 이제 nonlinear probing으로 넘어가며, 그곳에서 standard Gaussian이 유일한 optimum으로 등장함.

3.2 Nonlinear Probing
Pretrained encoder (f_\theta)를 더 유연하게 평가하기 위해 nonlinear probe를 쓰는 일이 점점 일반화되고 있음. 본 절에서는 널리 쓰이는 두 가지 nonlinear method를 분석함: 단순함 때문에 radius-based k-NN [Taunk et al., 2019, Sun and Huang, 2010, Zhang et al., 2017, Abu Alfeilat et al., 2019], 그리고 theoretical tractability 때문에 kernel method [Nadaraya, 1964, Watson, 1964]임.
Section 3.1과 마찬가지로, foundation model에 바람직한 embedding distribution이 무엇인지 묻는 것임.
먼저 prediction function을 정의함. Training data는 (N)개의 embedding과 training label의 쌍 ({(\mathbf{z}_n,\mathbf{y}n)}{n=1}^{N})으로 구성됨. Query vector (\mathbf{q})에 대해 radius-based k-NN을 사용한 prediction은 다음처럼 정의됨.
y^(q):=1∣Nr0(q)∣∑n∈Nr0(q)yn(kNN)\hat{\mathbf{y}}(\mathbf{q}) := \frac{1}{|\mathcal{N}_{r_0}(\mathbf{q})|} \sum_{n \in \mathcal{N}_{r_0}(\mathbf{q})} \mathbf{y}_n \qquad (\text{kNN})
여기서 (\mathcal{N}_{r_0}(\mathbf{q}) = {n:|\mathbf{z}_n-\mathbf{q}|\le r_0})임. Radius (r_0)의 구체적 선택은 query prediction을 만들 때 평균내는 neighbor의 수를 조절함.
Kernel method에서 query (\mathbf{q} \in \mathbb{R}^{K})에 대한 prediction은 다음과 같이 주어짐.
\(y^(q)≜∑n=1NKh(q−zn)yn∑n=1NKh(q−zn)(Kernel)\hat{\mathbf{y}}(\mathbf{q}) \triangleq \frac{\sum_{n=1}^{N} K_h(\mathbf{q}-\mathbf{z}_n)\mathbf{y}_n} {\sum_{n=1}^{N} K_h(\mathbf{q}-\mathbf{z}_n)} \qquad (\text{Kernel})\)
이제 total variance가 고정된 제약 하에서 (\mathbf{Z})의 모든 distribution에 대해 탐색함. 예를 들어,
\(Tr(Cov(Z))=κ1or∥Cov(Z)∥F=κ2\mathrm{Tr}(\mathrm{Cov}(\mathbf{Z}))=\kappa_1 \quad \text{or} \quad \|\mathrm{Cov}(\mathbf{Z})\|_F=\kappa_2\)
같은 constraint를 둠.
\(\kappa\)의 구체적 값은 optimal distribution의 shape에는 영향을 주지 않음.
Linear regime에서의 유도와 동일한 유형의 derivation을 따르되(몇 가지 추가 regularity condition을 제외하고), bias를 최소화하는 유일한 optimum이 isotropic Gaussian임을 정확히 식별할 수 있음. 이는 아래에서 formalize됨.
Numerous additional details and discussions on the regularity assumptions we employed are provided in Section A. 우리가 사용한 regularity assumption에 대한 추가적인 detail과 discussion은 Section A에 제공됨. 이 결과들을 종합하면, isotropic Gaussian distribution이 downstream task 전반에서 foundation model의 worst-case risk를 최소화하는 optimal design임이 정립됨.
3.3 Geometric and Practical Insights
Downstream task에 대한 정보가 전혀 없을 때도 isotropic Gaussian이 optimal임을 이제 empirical하게 검증함.
Linear probing(Section 3.1)에 집중하며, 여기서는 고려하는 모든 distribution이 동일한 total variance를 갖도록 맞춰짐.
Linear probe를 사용할 때, anisotropic distribution은 (Tikhonov regularization이 있을 때) bias와 variance를 모두 증가시킴.
먼저 bias(lemma 1)를 보면, Figure 18에서 continuous regression과 discrete classification task 모두에 대한 visualization을 제시함. Estimated parameter와 ground-truth parameter 사이의 cosine similarity는 isotropic distribution에서만 1이 됨을 관찰함. Anisotropic case에서는 sample size나 regularization strength와 무관하게 cosine similarity가 저하됨.
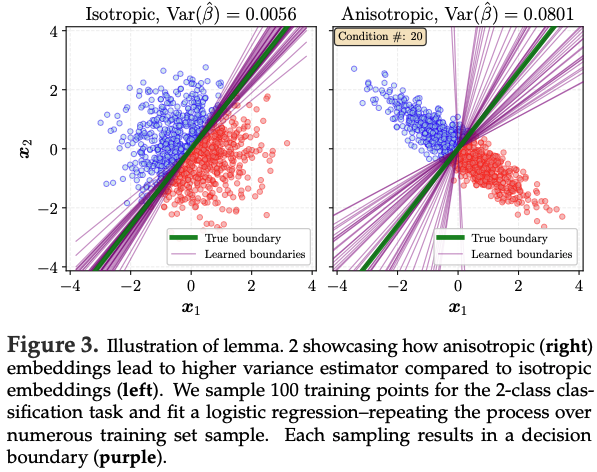
Variance(lemma 2)에 대해서는, Figure 3에서 covariance가 anisotropic(오른쪽)일 때 learned parameter가 isotropic(왼쪽)보다 training set에 따라 훨씬 크게 변동함을 보임. 이는 OLS 대신 logistic regression을 쓰더라도 동일함. Figure 17은 이 효과를 더 보여주며, 두 경우 모두에 대해 서로 다른 training sample에서 학습된 (\beta) parameter들의 distribution을 제시함. Anisotropic distribution이 명확히 더 높은-variance estimator를 생성함.
이 theoretical + empirical result는 LeJEPA를 위한 design principle을 정립함:
post-training 이후 마주칠 downstream task 전반에서 worst-case risk를 최소화하려면 embedding (f_\theta(\mathbf{x}))는 isotropic Gaussian distribution을 따라야 함.
Section 4에서는 이 distribution을 달성하기 위한 새로운 regularizer를 소개함.
4. SIGReg: Reliable Isotropic
Gaussian Regularization in
High-Dimension
Section 3에서 isotropic Gaussian을 optimal embedding distribution으로 정립했으므로, 이제 Sketched Isotropic Gaussian Regularization(SIGReg)를 소개함.
SIGReg는 distribution matching objective이며,
동시에 (i) differentiable, (ii) scalable, (iii) provable, (iv) interpretable하도록 설계됨.
SIGReg는 세 가지 핵심 innovation 위에 구축됨.
- 첫째, distribution matching을 null hypothesis \(P_\theta = Q\) 하에서의 statistical test로 formulation함(Section 4.1).
- 둘째, linear complexity와 efficient multi-GPU scaling을 유지하면서도 bounded gradient와 curvature를 보장하는 test를 식별함(Section 4.2).
- 셋째, SIGReg는 curse of dimensionality를 우회하여 collapsed shortcut solution을 완전히 제거함(Section 4.3).
4.1 Hypothesis Testing as a Judge
\(f_\theta(\mathbf{x})\)의 distribution \(P_\theta\)가 target distribution Q와 match되도록 요구하는 일은 보통 distance나 divergence의 다양한 measure를 만들고 이를 high-dimension에서 추정하는 방식으로 수행됨. 본 논문은 통계에 기반한 다른 출발점을 제안함.
다음 hypothesis testing framework를 고려함 [Fisher, 1928, Neyman and Pearson, 1933].
\(H0:Pθ=Qvs.H1:Pθ≠Q(2)H_0: P_\theta = Q \quad \text{vs.} \quad H_1: P_\theta \ne Q \qquad (2)\)
여기서 \(H_0\)는 null hypothesis로 불림. 즉, Equation (2)는 null을 기각할 만큼 충분한 empirical evidence가 있는지를 묻는 것임. 이를 답하기 위해 다음 절차를 따름.
- test-statistic을 사용함. 이는 empirical sample로부터의 evidence를 요약하는 단일 scalar value임.
- Type I error 확률 \(\alpha\)에 기반해 test-statistic의 critical value \(\tau_\alpha\)를 결정함. Type I error는 true null hypothesis를 잘못 기각하는 경우를 의미함.
- test-statistic을 \(\tau_\alpha\)와 비교함. test-statistic이 \(\tau_\alpha\)를 초과하면 null hypothesis를 기각함.
null이 기각되지 않는다면, \(P_\theta = Q\)에 반하는 충분한 empirical evidence가 없다고만 주장 가능함.
하지만 Equation (2)는 high-dimension에서 impractical함. 기존 test들은 고려하는 sample 수에 대해 최소 quadratic complexity를 가지기 때문임(자세한 내용은 Section F). 따라서 Equation (2)를 더 단순한 univariate test들로 분해하여 sketching strategy를 도출함.
Push-forward distribution을 다음처럼 표기함.
\(Pθ(a)≜(a⊤)#Pθ,Q(a)≜(a⊤)#QP_\theta^{(\mathbf{a})} \triangleq (\mathbf{a}^\top)_\# P_\theta, \qquad Q^{(\mathbf{a})} \triangleq (\mathbf{a}^\top)_\# Q\)
이를 이용해, 방향 (\mathbf{a})에 대한 directional univariate test를 다음처럼 정의함.
\(H0(a):Pθ(a)=Q(a)vs.H1(a):Pθ(a)≠Q(a)(3)H_0(\mathbf{a}): P_\theta^{(\mathbf{a})} = Q^{(\mathbf{a})} \quad \text{vs.} \)
\(\quad H_1(\mathbf{a}): P_\theta^{(\mathbf{a})} \ne Q^{(\mathbf{a})} \qquad (3)\)
여기서 (\mathbf{a} \in \mathcal{S}^{K-1})는 unit-norm directional vector임. Equation (3)에 대응하는 directional test-statistic은 다음처럼 계산됨.
\(T({a⊤fθ(xn)}n=1N)T\left(\left\{\mathbf{a}^\top f_\theta(\mathbf{x}_n)\right\}_{n=1}^{N}\right)\)
Test (T)의 예시는 이후 Section 4.2에서 제공됨. 이 과정을 (M)개의 direction 집합 (A \triangleq {\mathbf{a}_1,\ldots,\mathbf{a}_M})에 대해 반복하고, individual value를 aggregate하면 다음 global test-statistic을 얻음.
TA({fθ(xn)}n=1N)≜maxa∈AT({a⊤fθ(xn)}n=1N)(4)T_A\left(\left\{f_\theta(\mathbf{x}_n)\right\}_{n=1}^{N}\right) \triangleq \max_{\mathbf{a}\in A} T\left(\left\{\mathbf{a}^\top f_\theta(\mathbf{x}_n)\right\}_{n=1}^{N}\right) \qquad (4)
이제 Equation (4)가 Equation (2)의 original multivariate null hypothesis를 test하기에 consistent하다는 formal statement를 제공함. 이 결과는 well-known union-intersection principle [Roy, 1953]과, 약간 수정된 Cramér–Wold theorem을 활용함. 분포에서의 equality는 다음 기호로 표기함.
\(\overset{d}{=}\)
thm. 2의 proof에 필요한 assumption은 이후 Section 4.2에서 제시될, classical consistent univariate test (T)들에 대해 성립함.



4.2 SIGReg: Sketching the Epps-Pulley
Test is Stable and Scalable
본 논문이 제안하는 regularizer—Sketched Isotropic Gaussian Regularization(SIGReg)로 명명됨—는 thm. 2로부터 직접 도출됨.
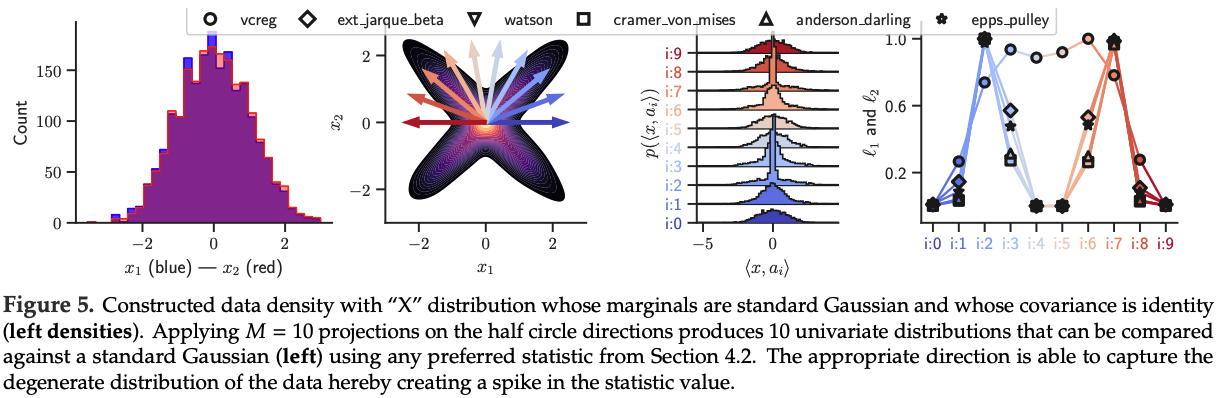
즉, isotropic Gaussian을 target으로 하는 어떤 statistical test (T)를 사용하든 thm. 2의 구성으로부터 SIGReg가 나오며, 이는 Figure 2와 Figure 5에 의해 illustration되고 아래에서 formalize됨.
thm. 2에서의 (\mathbf{a} \in A)에 대한 (\max)를 (SIGReg)에서는 평균으로 대체함. 이는 (A)의 direction들에 대해 sparse gradient가 생기는 것을 피하기 위함임.
이제 어떤 (T)를 선택할지에 대해 더 깊게 들어가며, 통계학에서 잘 알려진 candidate test들을 비교함.
이 test들은 (i) moment-based(Section 4.2.1), (ii) CDF-based(Section 4.2.2), (iii) CF-based(Section 4.2.3) statistic으로 분류되며, 최종적으로 Epps–Pulley statistic을 선택하는 근거가 제시됨.
4.2.1 Moments are Unstable and Insufficient
첫 번째로 고려하는 statistic family는 moment-based임. Standard Gaussian을 moment의 instantiation으로 두면, third/fourth moment—즉 skewness와 kurtosis—를 비교하는 Jarque–Bera [Jarque and Bera, 1980] test를 다음처럼 정의할 수 있음.
\[ JB(\mathbf{u}) \triangleq \frac{N}{6} \left( \mathrm{skew}(\mathbf{u})^2 + \left(\frac{\mathrm{kurt}(\mathbf{u})-3}{2}\right)^2 \right) \qquad \text{(Jarque–Bera)} \]
여기서 (\mathrm{skew})는 데이터로부터 계산되는 skewness이며
\[\mathrm{skew}\frac{1}{n}\sum_{i=1}^{n}\frac{(x_i-\hat{\mu})^3}{\hat{\sigma}^3}\]
(\mathrm{kurt})는 kurtosis이며
\[\mathrm{kurt}\frac{1}{n}\sum_{i=1}^{n}\frac{(x_i-\hat{\mu})^4}{\hat{\sigma}^4}\]
임. 보통 (Jarque–Bera) test는 어떤 mean/variance를 가지는 Gaussian을 따르는지 확인하기 위해 쓰이므로, moment 3과 4만 봄. 하지만 본 논문에서는 standard Gaussian test가 목표이므로, 첫 두 moment에 대한 usual statistic도 추가하여 extended test (EJB)를 정의함.
\[ EJB(\mathbf{u}) \triangleq \frac{N\hat{\mu}(\mathbf{u})^2}{\hat{\sigma}(\mathbf{u})^2} + \frac{(N-1)\left(\hat{\sigma}(\mathbf{u})^2-1\right)^2}{2} + JB(\mathbf{u}) \qquad \text{(Extended Jarque–Bera)} \]
(Extended Jarque–Bera)는 처음 네 개 moment에 대한 moment matching problem으로 작동함. 이런 moment matching method들은 statistical test뿐 아니라, data의 parametric/nonparametric model을 학습하는 수단으로도 강력함이 입증되어 왔음.
The Stability and Identifiability Conundrum.
이제 moment-based test가 강력하더라도 LeJEPA에는 적합하지 않은 이유를 설명함.
Distribution (P)의 (k)-th moment를 (m_k(P))로 표기함.
첫 번째 관찰은, Carleman condition
\[ \sum_{k=1}^{\infty} m_{2k}(Q)^{-1/(2k)}=\infty \quad \text{[Carleman, 1926]} \]
을 만족하는 well-behaved distribution(예: Gaussian) 또는 finite interval을 갖는 distribution [Hausdorff, 1923]은 moment들에 의해 uniquely 결정된다는 점임. 하지만 finite number의 moment만 사용하면, 통계학에서 잘 알려진 다음 non-identifiability issue가 발생하며, 이는 “모든 moment를 쓰자”는 동기의 근거로 자주 활용됨 [Lehmann and Romano, 2005].
따라서 thm. 3은 distribution matching을 정확하게 만들어 collapsed shortcut solution을 제거하기 위해 가능한 한 큰 (K)를 사용하라는 guideline을 제공함.
하지만 그렇게 하면 gradient norm이 (O(k))로 scaling되고, (k)-th moment에 대한 Monte Carlo gradient estimate의 variance가
\[ O!\left(k^2, m_2^{(k-1)}\right) \]
로 증가하여 gradient-based training이 불안정해짐.
이는 다음 관계 때문임:
\[ \nabla_\theta m_k!\left(P_\theta^{(\mathbf{a})}\right) \left| \mathbb{E}\left[ k,(\mathbf{a}^\top f_\theta(\mathbf{x}))^{k-1}, \mathbf{a}^\top J_{f_\theta}(\mathbf{x}) \right] \right| \]
여기서 (J_{f_\theta}(\mathbf{x}) \in \mathbb{R}^{K\times P})는 Jacobian matrix임.
결과적으로 training stability와 identifiability를 동시에 달성할 수 없는 impractical situation이 만들어짐.
4.2.2 Cumulative Density Functions are Impractical
두 번째 family는 CDF에 기반한 test임.
이 test들은 sorting이 필요하므로, N개 sample의 k-th order-statistic을 \(x_{k:N}\)로 표기함.
가장 표준적인 test 두 개는 서로 다른 weighting을 갖는 quadratic Empirical Density Function statistic이며, Cramér–von Mises [Cramér, 1928, Von Mises, 1981]와 Anderson–Darling [Anderson and Darling, 1952]로 알려져 있음.
이는 다음처럼 주어짐.
\[ T_w N\int_{-\infty}^{\infty} \left(F_N(x)-F(x)\right)^2, w(x), dF(x) ] [ w(x)=1 \qquad \text{(Cramér–von Mises)} ] [ w(x)=\left[F(x)\left(1-F(x)\right)\right]^{-1} \qquad \text{(Anderson–Darling)} \]
여기서 (w(x))는 weighting function임. Equation (Cramér–von Mises) 위에 (U^2) statistic을 추가하면 Watson test [Watson, 1961]가 복원됨.
\[ U^2 = T_w - N\left(\bar{F}-\frac{1}{2}\right)^2 \qquad \text{(Watson)} \]
Kolmogorov–Smirnov test [Kolmogorov, 1933]는 고려하지 않음. 이는 (\ell_2)-norm 대신 (\ell_\infty)-norm을 사용하여 sparse gradient를 만들기 때문임. 또 다른 흔한 test로 Shapiro–Wilk test [Shapiro and Wilk, 1965]가 있으나, 실험적으로 unstable함을 확인했으며 detail은 Section E에 제공됨.
Lack of Scalability and Differentiability.
CDF-based test는 sorting을 요구함. Sorting은 예컨대 (O(N\log N))의 Quicksort algorithm [Hoare, 1962]처럼 고도로 최적화되어 있지만, 그럼에도 SGD의 embarrassingly parallel한 성질을 깨뜨림.
특히 multi-GPU에서는 synchronization requirement 때문에 더 문제가 됨 [Tanasic et al., 2013, Maltenberger et al., 2022].
또한 이 test들은 sorting과 order statistic 같은 non-differentiable operation을 포함하므로, relaxation 없이는 gradient-based optimization에 부적합함 [Cuturi et al., 2019, Grover et al., 2019, Petersen et al., 2022].
물론 intricate sketching solution이 존재하긴 함 [Dunning and Ertl, 2019, Masson et al., 2019, Dunning, 2021]. 하지만 그런 solution들은 추가 hyperparameter를 다수 도입하며, 이는 LeJEPA의 첫 번째 motivation과 배치됨.


4.2.3 Characteristic Functions are Stable, Scalable and Identifiable
세 번째 test family는 Empirical Characteristic Function(ECF)에 관한 것이며, 이는 density function의 Fourier transform임. Epps–Pulley test [Epps and Pulley, 1983]는 가장 popular한 test 중 하나이며, 데이터의 ECF를 target CF와 weighted (\ell_2)-norm으로 단순 비교함.
\[ EP = N \int_{-\infty}^{\infty} \left| \hat{\phi}_X(t) - \phi(t) \right|^2 w(t), dt \qquad \text{(Epps–Pulley)} \]
첫 번째로 중요한 관찰은, ECF가 (\hat{\phi}X(t)=\frac{1}{n}\sum{j=1}^{n} e^{itX_j})로 정의된다는 점임.
이는 complex exponential의 단순 평균이므로, 자연스럽게 differentiable하고 distributed setting에서도 효율적인 all_reduce operation을 통해 쉽게 계산됨. Weight function은 보통 Gaussian이며, 예컨대 (w(t)=e^{-t^2/\sigma^2}) 같은 형태임. (\sigma)는 흔히 1로 설정됨.
Entropy [Székely and Rizzo, 2005] 기반 test 등 다른 test는 여기서 고려하지 않음.
이는 univariate entropy estimation을 위해 수많은 추가 design choice가 필요하기 때문임 [Silverman, 2018, Beirlant et al., 1997].
예를 들어 kernel을 쓰는 방식 [Joe, 1989]이나 M-estimator를 쓰는 방식 [Miller, 2003] 등이 요구됨.
Epps–Pulley는 bounded loss, gradient, curvature를 가짐. 이제 남은 두 family인 moment-based와 CDF-based와 비교 관점에서 이를 해석함.
먼저 moment는 데이터에 대한 polynomial이며, 더 높은 moment로 갈수록 growth rate가 극단적으로 커짐(존재한다는 가정 하에서조차 그러함). Well-behaved distribution에서도 값을 (k)제곱으로 올리는 것은 빠르게 exploding gradient로 이어질 수 있음. 이는 projected sample (z_i=\mathbf{a}^\top f_\theta(\mathbf{x}_n)), (n=1,\ldots,N)에 대해 ECF가 항상 bounded이고 어떤 input distribution에 대해서도 gradient가 bounded인 것과 뚜렷이 대비됨.
Chain rule에 의해 thm. 4는 곧바로 다음을 줌:
\[ \left|\nabla_\theta EP(\mathbf{a})\right| \le \frac{4 \sigma^2}{N} \sum_{i=1}^{N} \left| \mathbf{a}^\top \nabla_\theta f_\theta(x_i) \right| \]
따라서 stable gradient가 제공됨.
Moment-based 및 CDF-based test의 한계와 thm. 4를 함께 고려하면 (Epps–Pulley)를 선택하는 근거가 됨:
- (i) DDP-friendly하며 scalable함,
- (ii) input distribution과 무관하게 gradient와 curvature가 uniformly bounded됨,
- (iii) hyper-parameter free implementation이 가능함.
마지막으로, 본 구현은 minibatch size를 (N)이라 할 때 memory 및 computational complexity가 (\mathcal{O}(N))인 linear임을 강조함.
이 statistical test를 사용한 SIGReg 구현은 algorithm 1에 제시되며, forward-backward pass의 computation time은 Table 6에 제공됨.
LeJEPA를 소개하기 전 마지막 단계로, high-dimension에서 (2)가 효과적이려면 direction 수 (|A|)에 어떤 요구가 있는지 분석해야 함.
4.3 How SIGReg Beats the Curse of Dimensionality
본 절은 (SIGReg)가 효과적인 statistical test가 되기 위해 집합 (A)에서 얼마나 많은 slice를 sample해야 하는지를 규정하고자 함.
이는 LeJEPA가 isotropic Gaussian embedding으로 성공적으로 converge하기 위해 핵심적인 design임.
Smoothness Beats the Curse of Dimensionality
첫 번째 논거는 embedding dimension (K)에 대해 (|A|)가 유리하게 scaling된다는 주장에 기반하며, 이는 (P_\theta)의 Sobolev regularity (\alpha)로 측정되는 smoothness에 의존함 [Adams and Fournier, 2003].
아래에서는 test statistic이 (|A|=M)개의 direction에 대해 최소화될 때, Equation (3)의 directional test가 가능한 모든 direction (\mathbf{a})에 대해 어떻게 bound되는지를 formalize함.
유한한 direction 집합에서 EP test가 만족(0이 됨)될 때 random direction (\mathbf{a})에 대한 expected discrepancy의 bound를 제공함. 제시된 proof는 moment-based와 CDF-based test의 경우도 포함함.
\(|A|\to\infty\)일 때 bound는 \(|A|^{-2\alpha/(K-1)}\)로 decay함을 보이며, \(\alpha\)가 클 때 \(\epsilon\)-approximation에 \(|A|=\mathcal{O}(K)\)개의 direction이면 충분함을 보임.
\(\alpha\)가 다른 embedding density의 예시는 Figure 4에 제공됨.
다음 statement는 (M)개의 direction이 (\alpha)의 함수로서 전체 공간을 실제로 어떻게 constrain하는지를 특징지음.
상수
\[C(K,\alpha)\frac{2}{2^{2\alpha}\pi^{(K-1)/2}\Gamma!\left(\alpha+\frac{K-1}{2}\right)},(K-1)\Gamma(\alpha)\Gamma!\left(\frac{K-1}{2}\right)\]
는 Figure 15(왼쪽)에서 visualization되어 \(\alpha\)와 \(|A|\)의 상호작용을 보여줌. 말로 풀면, DN의 자연스러운 smoothness(architecture에서 오거나 training 중 쓰이는 implicit/explicit regularizer에서 기인함) 덕분에, \(|A|\)개의 direction에 SIGReg를 적용하는 것만으로도 전체 공간을 tight하게 constrain하는 데 충분할 수 있음을 얻음.
또한 \(\mathbf{a}\)에 대해 worst-case를 고려하거나, \(\mathbf{a}\)에 low-discrepancy sequence를 사용하더라도 asymptotic bound는 변하지 않음을 언급함. 자세한 내용은 Section D에 제공됨.
SGD Beats the Curse of Dimensionality
두 번째 논거는 DN training의 iterative nature를 활용함.
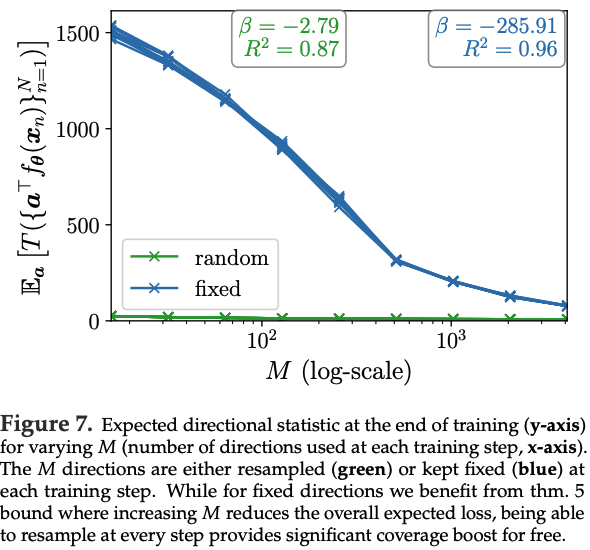
\(|A|\)를 수백 개 정도만 사용하더라도, 누적된 sampled direction 수는 training time에 따라 선형으로 증가함.
이 resampling effect(Figure 7 하단에 illustration됨)는 빠른 convergence를 가능하게 함.
작은 (|A|)에서도, minibatch 전체에 걸쳐 A를 고정하는 것에 비해(recall thm. 5) 더 tight한 distributional matching을 달성함.
실험에서는 (|A|=16)처럼 매우 작아도, 매 minibatch마다 resampling이 누적되는 효과 덕분에 (|A|)가 수천 단위인 fixed set보다 쉽게 outperform할 수 있음을 보임.
Empirical Validation on Synthetic Data
본 절은 gradient-based training으로 (SIGReg)를 적용하여 isotropic embedding을 생산하는 controlled experiment로 마무리함. 이 setup에서는 differentiable하게 만들고 최적화할 대상이 embedding (\mathbf{Z}) 자체임.
Embedding을 직접 최적화함으로써, architecture로부터 생길 수 있는 어떤 constraint나 regularization 없이 loss의 영향을 관찰할 수 있음.
(D)-dim 공간에서 (N)개의 i.i.d. sample (\mathbf{x}_n)을 sampling함.
이 sampling은 isotropic Gaussian distribution에 기반하지만, 처음 두 dimension은 adversarial “X” shape로 다시 설정됨.
즉 (D)개의 dimension 중 오직 두 개만 변형하면 되며, 나머지는 이미 isotropic Gaussian target distribution을 따르고 있음.
그 다음 sample (\mathbf{x}_n)을 differentiable하게 만들고, (M)개의 random direction에서 계산되는 다양한 statistical test의 값을 최소화하도록 이를 최적화함.
이 direction들은 각 gradient step 이후 resampling되며, 이는 LeJEPA에서 사용할 절차와 동일함.
Figure 6에서 결과를 제시하며, (D=512)이고 (M=16)인 challenging case에서도 SIGReg가 두 degenerate dimension을 탐지하고, target distribution 하에서의 형태로 다시 펼쳐(unfold) 되돌릴 수 있음을 보여줌.



5. LeJEPA: Stable and Scalable Implementation
Foundation model을 위한 optimal embedding distribution이 isotropic Gaussian임을 정립했고(Section 3), 이 distribution을 달성하기 위한 SIGReg를 도입했으므로(def. 2), 이제 complete LeJEPA framework를 제시함.
먼저 candidate statistical test를 평가하고(Sections 4.2.1, 4.2.2), gradient-based training에는 characteristic function 기반 test가 optimal임을 식별함(Section 4.2.3).
LeJEPA의 전체 구현은 Section 5.1에 이어짐.
5.1 LeJEPA: SIGReg + Prediction Loss
이제 SIGReg부터 시작하여 prediction loss와 total loss까지 포함하는 LeJEPA 구현을 논의함.
The SIGReg Loss.
Epps–Pulley를 선택함.
이는 provably bounded함(thm. 4)과 scalability 때문임.
구현은 적분을 제외하면 식을 그대로 따르며, 적분은 quadrature approximation으로 추정됨.
Figure 20의 ablation에서 보이듯, 단순한 trapezoidal quadrature rule만으로도 knot 수가 17개처럼 적어도 충분함을 확인함. 특히 integrand의 symmetry를 활용하여 knot 수를 공짜로 두 배로 늘릴 수 있으며(official code 참조), 이를 사용함.
한편 minibatch를 사용하면 bias가 도입되며, 그 bias는 (\mathcal{O}(1/N)) rate로 사라짐이 아래에서 formalize됨. 따라서 Epps–Pulley를 사용해 얻는 gradient는 명시적인 (\mathcal{O}(1/N)) term만큼 bias가 존재함. 이 bias는 minibatch가 16처럼 작아도 매우 작아서 문제가 되지 않음을 확인함.
Unbiased alternative로는 (|\phi_\theta|^2)에 대한 U-statistic debiasing이나 sample splitting이 포함되지만, 본 연구에서는 이를 탐구하지 않음. Epps–Pulley statistic을 사용한 SIGReg term의 최종 구현은 algorithm 1에 제공됨.
The Prediction Loss.
Notation을 표준화하기 위해 DINO [Caron et al., 2021]의 setup을 채택함.
즉 \(V_g\)개의 global view와 \(V_\ell\)개의 local view를 생성하여 총 view 수가 \(V=V_g+V_\ell\)가 되도록 함.
각 \(\mathbf{z}{n,v}\)의 index 중 \(1,\ldots,V_g\)를 global view로 설정함.
Local view가 없는 경우에는 \(V\ell=0\)으로 두면 됨.
Prediction loss는 “모든 view가 global view를 예측”하도록 정의되며 다음과 같음.
\[ \mathcal{L}{pred}\left({\mathbf{z}{n,v}}_{v=1}^{V}\right) \frac{1}{V_g}\sum_{v=1}^{V_g}\frac{1}{V}\sum_{v'=1}^{V} \left|\mathbf{z}{n,v}-\mathbf{z}{n,v'}\right|_2^2 \qquad (5) \]
이는 다음과 같이 변형될 수 있음.
\[ \frac{1}{V}\sum_{v'=1}^{V} \left| \frac{1}{V_g}\sum_{v=1}^{V_g}\mathbf{z}{n,v}-\mathbf{z}{n,v'} \right|_2^2 \qquad (6) \]
그리고 다음처럼 표기함.
\[ \triangleq \frac{1}{V}\sum_{v'=1}^{V} \left|\boldsymbol{\mu}n-\mathbf{z}{n,v'}\right|_2^2 \qquad (7) \]
여기서 \(\boldsymbol{\mu}n \triangleq \frac{1}{V_g}\sum{v=1}^{V_g}\mathbf{z}_{n,v}\)로 둠.
Equation (5)에서 Equation (6)으로의 유도는 Section B.6에 자세히 제공됨.
LeJEPA Loss.
최종 total loss는 위 prediction loss와, 각 view에 대해 적용되는 SIGReg를 단순히 결합한 형태임.
\[ \mathcal{L}{LeJEPA}\left({\mathbf{x}{n,v}}_{n,v=1}^{B,V}\right) \lambda\frac{1}{V}\sum_{v=1}^{V} SIGReg\left({{\mathbf{z}{n,v}}{n=1}^{B}}\right) + (1-\lambda)\frac{1}{B}\sum_{n=1}^{B} \mathcal{L}^{(V_g)}{pred}\left({\mathbf{z}{n,v}}_{v=1}^{V}\right) \qquad \text{(LeJEPA)} \]
(LeJEPA)의 구현은 algorithm 2에 제시됨.
전체 구현은 일반적인 model definition, optimizer, data loader를 제외하면 PyTorch에서 수십 줄 수준(algorithms 1, 2)만 필요함. Prototype, stop-gradient, teacher–student network가 없다는 점 때문에 (LeJEPA)는 매력적이며, prediction term과 isotropic Gaussian term 사이의 trade-off를 조절하는 단 하나의 hyperparameter (\\lambda\)만 포함함.





5.2 Relation to Prior Work
Section 6의 실험을 제시하기 전에, 본 절에서는 제안하는 LeJEPA와 SIGReg objective가 기존 문헌의 framework들과 어떻게 관련되는지 논의하며 마무리함.
JEPAs에서 이런 slicing 및 distribution matching을 사용하는 기존 solution은 없지만, generative model 및 optimal transport에는 유사한 pipeline이 존재함. 대표적으로 Sliced Score Matching [Song et al., 2020]은 generative model에서 density estimation을 쉽게 하기 위해 공간을 univariate slicing하는 방식을 활용하자고 제안함. 비슷한 맥락에서 sliced Wasserstein distance [Bonneel et al., 2015, Nguyen and Ho, 2023] 역시 이러한 전략을 사용하여 optimal transport를 더 빠르고 더 잘 수행하도록 함.
또한 (Epps–Pulley) test의 integral을 본 논문처럼 quadrature로 근사하는 대신 정확히 계산한다면, 각 slice loss 값은 두 distribution 사이의 distance를 측정하는 kernel MMD [Sriperumbudur et al., 2010, Gretton et al., 2012, Chwialkowski et al., 2016]를 복원함. 다만 이는 quadratic complexity를 갖는 형태로 나타남.
마지막으로, (Epps–Pulley) 대신 특정 test를 사용해 LeJEPA를 구성하면 limit에서 일부 기존 SSL framework를 복원할 수도 있음. 예를 들어,
\[T({x_n}_{n=1}^{B})\mathrm{mean}({x_n}{n=1}^{B})^2+\left(\mathrm{std}({x_n}{n=1}^{B})-1\right)^2\]
로 두고, 이 (T)를 LeJEPA에서 SIGReg와 함께 사용하면 slice 수가 매우 큰 limit에서 VICReg SSL method를 복원하게 됨.
사실 SIGReg는 기대값 관점에서 (E[Z]=0) 및 (\mathrm{Cov}(Z)=I_d)를 강제하게 됨. 여기서 (I_d)는 (d\times d) identity matrix이며, 유도는 Section B.14에 제공됨. 그리고 invariance term이 단순히 view embedding들 사이의 (\ell_2) distance이므로, 이 degenerate statistical test에 대해 LeJEPA는 VICReg를 복원하게 됨.
하지만 thm. 3에 근거하여, 이런 설정은 shortcut solution으로 이어지므로 강하게 반대함. 이는 VICReg에서도 이미 관찰된 현상임.
6. LeJEPA: Empirical Validation
이제 Section 5.1에서 설명한 LeJEPA 구현을 사용하여 comprehensive experiment로 그 효과를 보여줌.
LeJEPA가 다음을 만족함을 보임:
(i) 다양한 architecture와 dataset에서 reliably training됨(Section 6.1),
(ii) model selection에 유용한 informative training loss를 제공함(Section 6.2),
(iii) small-scale in-domain pretraining에서 frontier vision model을 outperform함(Section 6.3),
(iv) ImageNet-1k에서 parameter 수가 거의 10억에 달하는 규모까지 성공적으로 scale됨(Section 6.4),
(v) explicit supervision 없이도 rich semantic segmentation feature를 학습함.
6.1 LeJEPA’s Stability Across
Hyper-Parameters and Architectures
이제 LeJEPA가 hyperparameter, architecture, 그리고 experimental setup 전반에서 안정적임을 보임.
Cross-domain stability에 대한 추가 결과는 Section 6.3에 제시됨.
Stability across standard hyperparameters.
먼저 ImageNet-100과 ImageNet-1K에서 LeJEPA를 평가함. ImageNet-100에서는 ResNet-50을 학습하고, view 수와 loss weighting (\lambda)를 변화시킴(Figure 8). 두 축 모두에서 성능이 안정적으로 유지됨. 이에 따라 (\lambda=0.05)를 robust default로 추천함.
ImageNet-1K에서는 ViT-Large/14를 학습하고, batch size 및 global view 수 (V_g)와 local view 수 (V_\ell)를 탐색함(Table 1b). 기존 연구에서 흔히 쓰이던 설정인 \((V_g=2,\ V_\ell=8)\)이 LeJEPA에도 잘 transfer됨을 확인함.
특히 LeJEPA는 ImageNet-1K에서 batch size가 128처럼 작아도 competitive performance를 달성함(Table 1c). 이는 기존 method 대비 memory requirement가 줄어들 수 있음을 시사함.
따라서 시작점으로 lambda=0.05, \(V_g=2\), \(V_\ell=8\), 그리고 batch size \(\ge 128\)을 추천함.
Stability across Epps-Pulley hyperparameters.
다음으로 LeJEPA에 특화된 hyperparameter를 점검함. 즉 SIGReg에서 slice 수 (|\mathcal{A}|), Epps–Pulley test의 integration domain, 그리고 numerical integration을 위한 quadrature point 수를 살펴봄. Table 1a는 ViT-Large/14로 ImageNet-1K에서 수행한 ablation을 보여줌. Integration domain과 quadrature point 수는 성능에 거의 영향을 주지 않음을 확인함. 이는 기대되는 결과임. Characteristic function은 0에서 정확하므로, modest한 integration range만으로도 distribution의 moment들이 충분히 잘 characterise되기 때문임.
Slice 수 (|\mathcal{A}|)는 modest한 영향을 보임. Slice를 늘리면 성능이 약간 개선되지만, 512 slice만으로도 competitive result를 얻음.
따라서 시작점으로 integration point 17개, integration domain [-5,5], 그리고 slice 1024개를 추천함.

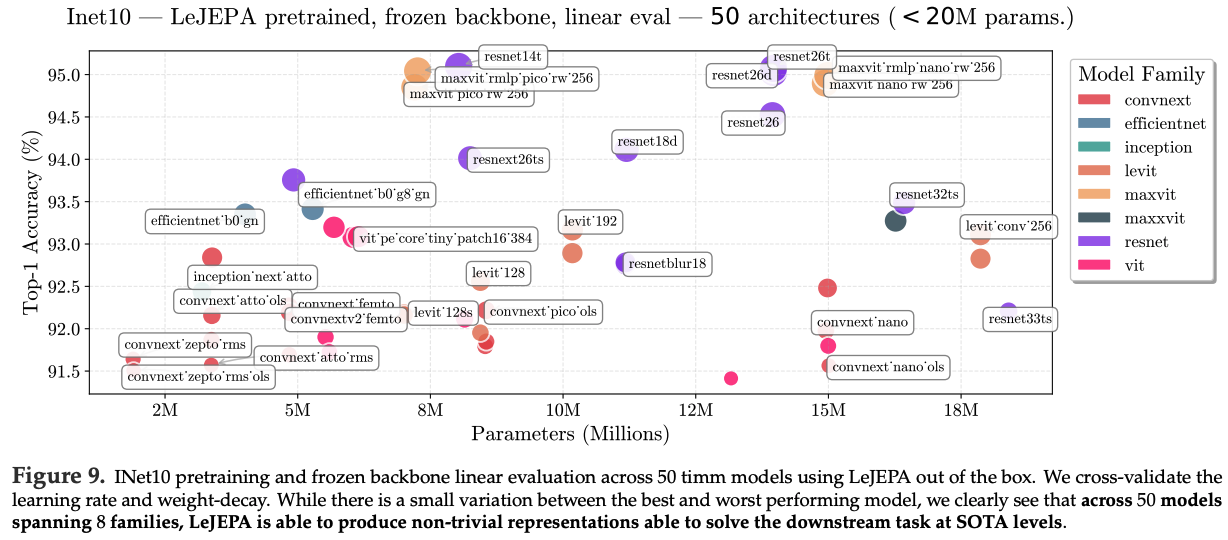
Stability across architectures.
LeJEPA의 핵심 장점 중 하나는 최근 method들(예: IJEPA, DINOv2) 대비 architecture-agnostic design임.
대부분의 modern self-supervised method는 Vision Transformer에 맞춰 tailoring되는 반면, LeJEPA는 수정 없이도 다양한 architecture family에서 동작함.
이를 검증하기 위해 ImageNet-10에서 8개 family에 속한 약 50개 architecture를 pretrain함.
선택 기준은 timm library의 model 중 parameter가 20M 미만인 모든 model임.
모든 model이 high-quality representation을 학습할 수 있었고, frozen backbone linear probing에서 top-1 accuracy가 91.5%~95% 범위에 도달함.
Supervised learning setup에서 성능이 좋은 model들이 LeJEPA에서도 선호되는 경향을 보이며, 예컨대 ResNet과 ViT가 그러함.
따라서 EfficientNet 같은 specialized model보다 ResNet, ViT 같은 standard architecture를 starting point로 사용하는 것을 추천함.
architecture-agnostic: 특정 아키텍처(ViT 등)에 맞춰 튜닝된 게 아니라, ResNet/ConvNet/ViT 등 여러 아키텍처에서 그대로 동작함
Removal of popular heuristics.
LeJEPA는 model과 dataset 전반에서 reliable performance를 제공할 뿐 아니라, provable construction 덕분에 collapse 방지를 위해 전통적으로 사용되던 많은 heuristic을 제거할 수 있음.
먼저 prior work는 image JEPA에서 predictor(비대칭 정보가 없는 경우)와 teacher–student architecture가 주로 collapse를 방지하기 위해 존재함을 empirical 및 theoretical하게 보여줌 [Grill et al., 2020, Jing et al., 2021, Tian et al., 2021, Caron et al., 2021, Chen et al., 2021]. 이 구성요소들을 제거하면 chance-level 성능을 보이는 collapsed encoder가 생성됨.
하지만 LeJEPA의 SIGReg loss 덕분에 predictor와 teacher–student architecture를 둘 다 제거해도 collapse가 발생하지 않음을 Table 4에서 보임.
Teacher–student configuration은 ViT model에서 small performance boost를 제공하긴 함.
이는 supervised learning에서 Stochastic Weight Averaging(SWA) [Izmailov et al., 2019]로 관찰되는 것과 일관됨.
그러나 collapse를 막는 데 필수는 아님.
본 setup에서는 Equation (6)에서 \(\mu\)를 생성하는 encoder에 SWA를 적용함.
둘째, recent work는 vision model에서 training instability를 막기 위해 register token이 필요함을 보였음 [Oquab et al., 2023, Siméoni et al., 2025, Darcet et al., 2023].
Table 1에서, 이런 instability는 training objective가 poorly conditioned하기 때문에 발생했을 가능성이 큼을 보임.
반면 LeJEPA는 register token이 필요하지 않으며, 있든 없든 stable performance를 달성함.
따라서 predictor나 register token 없이 training하는 것을 추천하며, ViT에서는 추가 성능 향상을 위해 optional하게 SWA를 적용하는 것을 추천함.
6.2 LeJEPA’s Training Loss is Informative of Downstream Performance
SSL pretraining의 주요 challenge는 학습된 representation의 quality를 전달하는 reliable signal이 부족하다는 점임. 그 결과, 흔히 supervised downstream task 성능을 모니터링하고, 때로는 unsupervised embedding statistic으로 보완함 [Agrawal et al., 2022, Garrido et al., 2023, Thilak et al., 2023]. 하지만 이 과정은 labeled data를 요구하며, 이는 비용이 크고 지나치게 specialized되어 있어 제한적임. 이 문제는 최신 JEPA model에서 더 악화됨. 최신 JEPA에서는 training loss가 downstream performance와 correlation이 낮고, training 동안 monotonic하게 감소하지 않을 수도 있음.
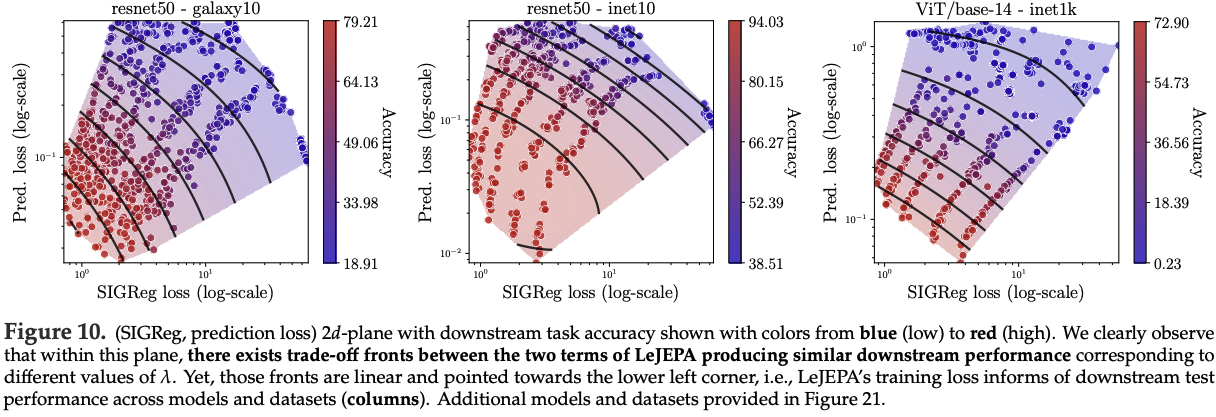
반면 LeJEPA에서는 training loss가 훨씬 유리하게 동작하여 model quality에 대한 meaningful signal을 제공함을 확인함. 먼저 Figure 10에서 SIGReg loss와 prediction loss가 span하는 2D plane을 제시하며, downstream task accuracy와의 뚜렷한 trend가 관찰됨.
더 인상적인 점은, mixing coefficient (\lambda)를 갖는 결합 training loss (LeJEPA)가 downstream accuracy와 매우 높은 Spearman correlation [Spearman, 1961]—(\rho_s)로 표기됨—을 보인다는 사실임. 그 값은 약 85%이며, 이는 strong signal로 간주됨. 이 강한 관계는 dataset과 architecture 전반에서 유지됨. 따라서 더 낮은 LeJEPA training loss는 더 좋은 downstream performance를 안정적으로 지시함.
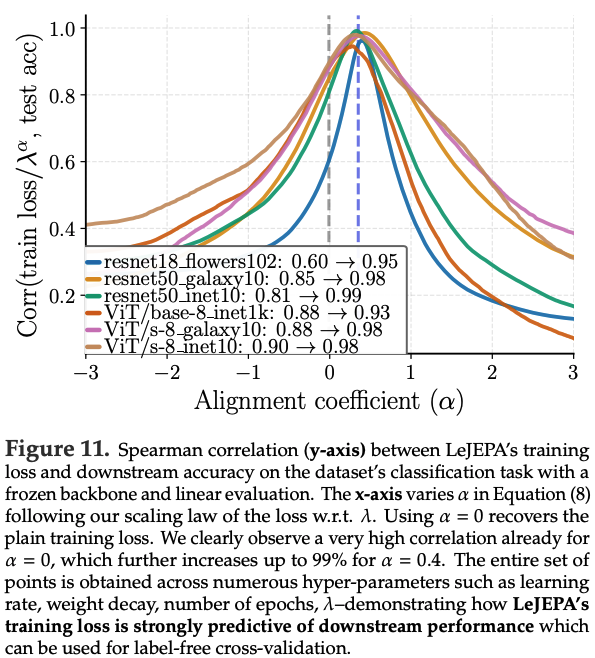
이 correlation은 trade-off weighting hyperparameter (\lambda)에 기반한 간단한 scaling law로 더 개선될 수 있음.
\[ C^{(\alpha)} \rho_s!\left( \frac{\text{train_loss}}{\lambda^\alpha}, \ \text{test_accuracy} \right) \qquad (8) \]
(\alpha \approx 0.4)로 설정하면, LeJEPA training loss는 여러 dataset과 model 전반에서 downstream performance와 nearly 99% correlation을 달성할 수 있음.
Figure 11에서 여러 dataset과 model에 대해 (C^{(\alpha)})가 (\alpha)의 함수로 어떻게 변하는지 보여주며,
Figure 19에서는 training LeJEPA loss와 downstream performance의 관계를 제시함.
LeJEPA training loss와 model quality 사이의 강한 alignment는 label-free SSL model selection과 cross-validation을 가능하게 함.

6.3 In-Domain LeJEPA Outperforms Frontier Model Transfer Learning
Self-supervised learning의 핵심 promise는 task와 domain 전반에서 generalize되는 universal representation을 학습하는 것임.
하지만 현재 frontier foundation model(예: DINOv2/v3, IJEPA)은 natural image에서 pretrain되어 있어, specialized domain의 practitioner는 supervised finetuning을 위해 많은 label을 수집해야만 함.
실제로 대부분의 frontier model은 그 domain에서 직접 training되기 어려움. Sample 수가 작을 수 있고, hyper-parameter를 다시 탐색하는 과정이 번거롭지만 필요하기 때문임 [Assran et al., 2022].
이런 pain-point를 LeJEPA가 어떻게 해결할 수 있는지 보여주기 위해, loss나 pretraining pipeline을 전혀 바꾸지 않고 새로운 domain에서 직접 pretrain하는 실험을 제안함.
Galaxy10 dataset을 선택함. 이는 galaxy morphology classification task이며, visual structure와 statistical property 양쪽에서 natural image와 크게 다름 [Balestriero et al., 2025]. 이 dataset은 10개 galaxy type에 대해 11,000개의 training sample을 포함함.
LeJEPA에서는 default hyper-parameter를 사용하고, 다양한 backbone을 400 epoch 동안 pretrain함.
비교 대상으로 최신 DINOv2, DINOv3, IJEPA를 사용함.
Figure 12에서 frozen backbone linear probing과 full-finetuning 모두에 대해 top-1 accuracy를 보고함. In-domain pretraining을 수행한 LeJEPA가 linear probing과 full finetuning 양쪽 모두에서 state-of-the-art frontier model(DINOv2, DINOv3)을 크게 outperform함을 관찰함.
추가 dataset과 backbone 결과는 Table 5에 제공되며, sample이 1000개인 dataset(flowers102)에서도 LeJEPA가 in-domain training을 수행할 수 있음을 보여줌.
이 결과를 LeJEPA의 architecture/hyper-parameter 안정성과 결합하면, 최신 frontier model이 아직 커버하지 못하는 domain에서 유망한 alternative가 될 수 있음을 시사함.
6.4 LeJEPA Scales Across Data and Models
이제 더 큰 pretraining dataset인 ImageNet-1k, 그리고 더 큰 backbone(예: ViT/Large(0.3B), ConvNextV2-Huge(0.6B))에 LeJEPA를 적용함.
이 두 model에 대해 inet1k에서 online linear probe accuracy가 각각 77.1%, 78.5%에 도달함.
In-distribution 성능을 넘어서 transfer learning도 탐색함.
Baseline으로는 setup이 가장 유사한 ViT-Huge(0.6B) 기반 IJEPA를 사용함.
또한 추가 stochastic prediction task [Bar et al., 2023]를 포함한 IJEPA의 개선 버전인 IJEPA + STOP도 포함함. LeJEPA는 Section 6.1에서 설명한 동일 recipe를 사용하고, frozen backbone으로 transfer learning 성능을 Table 2에 보고함.
더 작은 model과 더 짧은 training schedule을 사용했음에도 IJEPA를 consistent하게 outperform함을 관찰함.
Top-1 accuracy 외에도, Section 6.2에서의 LeJEPA training loss quality에 대한 관찰을 다시 확인함.
본 setup에서는 training curve가 매우 stable하고 smooth하게 나타나며, 이는 optimization landscape가 안정적임을 시사하고 careful한 hyperparameter selection의 필요를 제거함(recall thm. 4).
ViT-gigantic(1.8B parameters) 예시는 Figure 1에 제공됨.
6.5 Emergent Semantic Structure in LeJEPA Representations
성공적인 self-supervised learning의 hallmark는 explicit supervision 없이도 semantically meaningful한 attention pattern이 emergence되는 것임 [Caron et al., 2021]. LeJEPA가 이런 structure를 학습하는지 평가하기 위해, 학습된 representation의 attention map을 visualize함.
DINO [Caron et al., 2021]를 따라 embedding에 PCA를 적용하고, 첫 principal component들을 visualize함. 이 결과 object boundary 및 salient region과의 명확한 correspondence가 드러남(Figure 14).
또한 이 attention pattern이 unsupervised video segmentation을 가능하게 하는지도 탐색함. 이는 temporal consistency와 object understanding을 요구하는 challenging task임. [CLS] token의 self-attention map을 thresholding하여 binary mask를 얻고, training 동안 segmentation label 없이도 frame 간 object를 track하도록 함.
Figure 13에서 보이듯 LeJEPA의 attention은 foreground object를 background로부터 자연스럽게 segment하며, 뛰어난 temporal coherence를 보임.
이는 학습된 representation이 spatial semantics와 temporal structure를 모두 포착함을 시사함.
이런 emergent capability는 LeJEPA의 stability-focused objective가 learned feature의 semantic richness를 희생하지 않음을 보여줌.
7. Conclusion
JEPA 기반 self-supervised learning을 위한 principled theoretical framework를 정립했으며, 이는 JEPA의 핵심 pathology를 근본적으로 해결함.
기여는 theory와 practice를 모두 포괄함.
Isotropic Gaussian embedding이 worst-case downstream risk를 uniquely 최소화함을 증명했고, 이 distribution을 enforce하기 위한 tractable하며 provably correct한 방법으로 SIGReg를 도입했으며, 이 접근이 representational collapse를 design 차원에서 제거함을 보였음.
즉, teacher–student network, stop-gradient, asymmetric architecture 같은 ad-hoc 조합에 의존하지 않게 됨.
LeJEPA는 domain 전반과 60개 이상의 architecture에서 검증했으며, 1.8B parameter의 gigantic version까지 포함함.
단순함에도 불구하고, LeJEPA는 state-of-the-art 성능과 match되며 core implementation이 50줄 미만으로 가능함.
결정적으로, 본 접근은 SSL이 오랫동안 필요로 해온 것을 제공함.
즉, 실용적 algorithm design을 직접적으로 안내하는 mathematically rigorous foundation을 제공함.




I-JEPA와의 차이점은 LeJEPA
이 둘의 차이를 **"숙련된 정비공"과 "엔진 설계 공학자"** 의 비유로 설명해 드리겠습니다.
* **I-JEPA는 '숙련된 정비공'입니다.**
* **문제:** "자동차가 자꾸 시동이 꺼져요 (표현 붕괴가 일어나요)."
* **해결책:** 정비공은 자신의 풍부한 경험(Empirical Knowledge)을 바탕으로 문제를 해결합니다. "아, 이 모델(차종)은 이런 문제가 잦지. 여기에 **보조 부품(Teacher 네트워크)**을 달고, 이 배선(**Stop-Gradient**)을 끊어주면 해결될 거야." 이 방법은 효과적이지만, 왜 효과가 있는지에 대한 근본적인 설명보다는 **'경험에서 나온 비법(Heuristic)'** 에 가깝습니다.
* **LeJEPA는 '엔진 설계 공학자'입니다.**
* **문제:** "애초에 시동이 절대 꺼지지 않는 완벽한 엔진을 설계하려면 어떻게 해야 할까?"
* **해결책:** 공학자는 열역학 제1법칙 같은 **근본 원리(First Principles)**에서 출발합니다. "수학적으로 증명해보니, 엔진이 최적의 상태를 유지하려면 연료와 공기의 혼합비가 항상 **이상적인 비율(등방성 가우시안 분포)**을 유지해야만 한다. 나는 이 비율을 강제로 유지시키는 **'최첨단 제어 시스템(SIGReg)'** 을 설계하겠다." 이제 엔진은 구조적으로 시동이 꺼지는 것이 불가능해집니다.
---
이 비유를 바탕으로, 두 모델의 구체적인 차이점을 표로 정리하면 다음과 같습니다.
| 구분 | **I-JEPA (경험적 해결책)** | **LeJEPA (이론적 해결책)** |
| :--- | :--- | :--- |
| **핵심 철학** | **경험주의 (Empiricism):** 효과가 입증된 복잡한 장치들을 사용하여 문제를 해결한다. | **이론 우선주의 (Theory-First):** 문제의 근본 원인을 수학적으로 증명하고, 그에 기반한 단순한 해결책을 설계한다. |
| **표현 붕괴 방지법** | **구조적/경험적 장치 (Heuristics):** <br>• **Teacher-Student 네트워크**<br>• **Stop-Gradient**<br>• 모멘텀 인코더 (EMA) | **수학적 제약 (Mathematical Constraint):**<br>• **SIGReg 손실 함수**<br>• 임베딩 분포를 '등방성 가우시안'으로 직접 강제 |
| **구조 복잡도** | **복잡함 (Complex):**<br>실제 학습하는 Student 외에, 보조적인 Teacher 네트워크가 추가로 필요하다. | **단순함 (Lean):**<br>단 하나의 인코더 네트워크만 존재한다. 코드가 매우 짧고 직관적이다. |
| **안정성/견고함** | **상대적으로 예민함:**<br>Teacher를 업데이트하는 EMA 스케줄 같은 하이퍼파라미터에 성능이 민감할 수 있다. | **매우 견고함 (Robust):**<br>핵심 하이퍼파라미터 `λ` 하나만 있으며, 넓은 범위에서 안정적인 성능을 보인다. |
| **아키텍처 의존성** | **ViT 중심적:**<br>주로 ViT 아키텍처에서 그 효과가 입증되고 최적화되었다. | **아키텍처와 무관 (Agnostic):**<br>ViT, ResNet, ConvNeXt 등 어떤 종류의 아키텍처에서도 일관되게 잘 작동함을 증명했다. |
---
### 가장 중요한 차이점 요약
**1. 붕괴를 막는 방식의 차이:**
* **I-JEPA:** Student가 Teacher를 너무 빨리 따라잡지 못하도록, **천천히 움직이는 '목표물(Teacher)'**을 만들어주는 구조적인 트릭을 사용합니다.
* **LeJEPA:** "목표물을 움직이는" 간접적인 방식 대신, 임베딩 공간 전체에 **"절대 뭉치지 마라, 그리고 이 아름다운 구(球) 모양을 유지해라!"** 는 강력한 수학적 규칙(SIGReg)을 직접 부과합니다.
**2. 단순함과 범용성의 차이:**
* **I-JEPA:** Teacher-Student 구조 때문에 구현이 상대적으로 복잡하고, ViT라는 특정 아키텍처에 강하게 연결되어 있습니다.
* **LeJEPA:** 이 복잡한 구조를 모두 제거했기 때문에 **구현이 극도로 단순**하며, 그 원리가 수학에 기반하기 때문에 **어떤 아키텍처에도 이식 가능한 범용성**을 갖습니다.
**결론적으로, I-JEPA가 "JEPA라는 훌륭한 아이디어를 현실에서 작동하게 만든 최초의 성공적인 구현체"라면, LeJEPA는 "I-JEPA가 남겨둔 '왜 이 트릭들이 필요한가?'라는 근본적인 질문에 대한 이론적인 답을 제시하고, 그 답을 통해 훨씬 더 단순하고 강력하며 보편적인 완성형을 만들어낸 것"이라고 할 수 있습니다.**
Epps-Pulley 테스트
### Epps-Pulley 테스트: 정의와 목적
**Epps-Pulley 테스트**는 통계학에서 주어진 데이터 샘플이 **특정 확률 분포(여기서는 정규분포)**를 따르는지를 검정하기 위한 **'적합도 검정(Goodness-of-Fit Test)'** 방법 중 하나입니다.
이 테스트의 핵심적인 목적은 두 분포가 같은지를 비교하는 것인데, 이때 **특성 함수(Characteristic Function, CF)** 라는 강력한 수학적 도구를 사용합니다.
### 핵심 도구: 특성 함수 (Characteristic Function, CF)
특성 함수는 확률 분포를 완벽하게 정의하는 또 다른 방법입니다. 우리가 흔히 아는 확률 밀도 함수(PDF)나 누적 분포 함수(CDF)와는 다른 관점에서 분포를 바라봅니다.
* **정의:** 확률 변수 `X`의 특성 함수 `φ_X(t)`는 다음과 같이 정의됩니다.
`φ_X(t) = E[e^(itX)] = ∫ e^(itx) p(x) dx`
여기서 `E`는 기댓값, `i`는 허수 단위, `t`는 실수 변수(주파수 영역으로 해석 가능), `p(x)`는 `X`의 확률 밀도 함수입니다.
* **가장 중요한 성질 (유일성 정리):**
> **두 확률 분포의 특성 함수가 모든 `t`에 대해 동일하다면, 그 두 확률 분포는 완전히 동일하다.**
이 성질이 Epps-Pulley 테스트의 이론적 기반입니다. 즉, 특성 함수는 분포의 **'고유한 지문(fingerprint)'** 과 같습니다. 두 지문이 일치하면, 두 사람은 같은 사람입니다.
### Epps-Pulley 테스트의 작동 원리
Epps-Pulley 테스트는 이 '지문 비교' 원리를 사용하여, 우리 데이터 샘플의 '지문'과 목표 분포(정규분포)의 '지문'이 얼마나 다른지를 측정합니다.
#### **1단계: 두 개의 특성 함수를 준비한다**
1. **경험적 특성 함수 (Empirical Characteristic Function, ECF) - `φ_n(t)`:**
* **정의:** 우리가 가진 `n`개의 데이터 샘플 `{x_1, x_2, ..., x_n}`로부터 직접 계산한 특성 함수입니다.
* **수식:** `φ_n(t) = (1/n) * Σ[k=1 to n] e^(itx_k)`
* **의미:** 이것이 바로 우리 데이터 샘플의 **'실측 지문'** 입니다.
2. **이론적 특성 함수 (Theoretical Characteristic Function) - `φ_θ(t)`:**
* **정의:** 우리가 비교하고자 하는 목표 분포, 즉 **표준 정규분포 `N(0, 1)`** 의 특성 함수입니다.
* **수식:** 표준 정규분포의 특성 함수는 `φ_N(0,1)(t) = e^(-t²/2)` 라는 아름다운 형태로 이미 수학적으로 잘 알려져 있습니다.
* **의미:** 이것이 바로 우리가 대조해야 할 **'원본 정답 지문'** 입니다.
#### **2단계: 두 특성 함수의 '거리'를 측정한다**
이제 두 '지문'이 얼마나 다른지를 정량적으로 측정해야 합니다. Epps-Pulley 테스트는 두 함수 사이의 **'가중 제곱 거리(Weighted Squared Distance)'** 를 측정 통계량(Test Statistic)으로 사용합니다.
* **측정 통계량 `T_n`의 정의:**
`T_n = n * ∫ |φ_n(t) - φ_θ(t)|² w(t) dt`
* **각 요소의 의미:**
* `n`: 샘플 크기. 거리를 정규화하는 역할을 합니다.
* `|φ_n(t) - φ_θ(t)|²`: 특정 주파수 `t`에서, 두 지문의 차이를 제곱한 값입니다. 즉, 해당 주파수에서의 '불일치 정도'를 나타냅니다.
* `w(t)`: **가중 함수(Weighting Function)** 입니다. 모든 주파수 `t`를 똑같이 중요하게 보지 않고, 특정 주파수 영역의 불일치에 더 큰 가중치를 부여하기 위해 사용됩니다. Epps-Pulley 테스트는 보통 `w(t) = e^(-σ²t²)` 와 같은 가우시안 형태의 가중 함수를 사용하여, 원점(`t=0`) 근처의 저주파 영역(분포의 전체적인 모양을 결정)에 더 큰 중요도를 둡니다.
* `∫ ... dt`: **적분(Integral)** 입니다. 특정 주파수 `t`에서의 불일치만 보는 것이 아니라, **모든 주파수 영역에 걸쳐서** 측정된 '가중된 불일치 정도'를 **전부 합산**하여 최종적인 단일 숫자 값, 즉 '총 불일치 점수' `T_n`을 계산합니다.
#### **3단계: 판정 (딥러닝에서의 활용)**
* **통계학에서의 판정:** 계산된 `T_n` 값이 미리 정해진 임계값(critical value)보다 크면 "두 분포는 다르다"고 판정하고, 작으면 "다르다고 말할 증거가 불충분하다"고 판정합니다.
* **LeJEPA에서의 활용 (더 중요):** LeJEPA는 이 `T_n` 값을 **손실 함수(Loss Function)** 로 직접 사용합니다. 모델의 목표는 이 `T_n` 값을 **0으로 최소화**하는 것입니다. `T_n`이 0이 된다는 것은, 적분 안의 `|φ_n(t) - φ_θ(t)|²` 부분이 모든 `t`에 대해 0이 된다는 것을 의미하며, 이는 곧 우리 데이터의 특성 함수(`φ_n(t)`)가 목표인 정규분포의 특성 함수(`φ_θ(t)`)와 완벽하게 일치하게 됨을 의미합니다. 그리고 특성 함수의 유일성 정리에 따라, 이는 **우리 데이터의 분포가 정규분포와 같아짐**을 보장합니다.
---
요약
Epps-Pulley 테스트는:
1. 분포의 모든 정보를 담고 있는 **'특성 함수'** 라는 수학적 도구를 사용합니다.
2. 우리 데이터 샘플의 **'경험적 특성 함수'** 와 목표 분포(정규분포)의 **'이론적 특성 함수'** 를 계산합니다.
3. 모든 주파수 영역에 걸쳐 두 특성 함수의 **'가중 제곱 거리'를 적분**하여, 두 분포 사이의 전체적인 불일치 정도를 나타내는 단일 값(`T_n`)을 계산합니다.
4. LeJEPA는 이 `T_n` 값을 손실 함수로 사용하여, **이 값을 0으로 최소화하도록 모델을 학습**시킴으로써, 임베딩 분포가 목표인 정규분포를 따르도록 강제합니다.
모든 방향으로 프로젝션(projection)한 1차원 분포가 목표 분포(가우시안)의 프로젝션과 똑같아야만, 원래의 고차원 분포도 목표 분포와 똑같다고 보장.
모든 방향으로 프로젝션(projection)한 1차원 분포가 목표 분포(가우시안)의 프로젝션과 똑같아야만, 원래의 고차원 분포도 목표 분포와 똑같다고 보장할 수 있습니다.
사용자님께서 인용하신 "특성 함수의 유일성 정리"는 **1차원**에 대한 이야기입니다. LeJEPA는 이 1차원에서의 강력한 정리를, 고차원으로 확장하기 위해 또 다른 매우 중요한 수학 정리인 **"크라메르-볼트 정리(Cramér-Wold Theorem)"** 를 사용합니다.
이것을 "3D 물체의 정체 파악하기" 비유로 설명해 드리겠습니다.
---
### 크라메르-볼트 정리: "모든 그림자가 똑같으면, 실체도 똑같다"
* **문제:** 눈앞에 정체를 알 수 없는 반투명한 3D 물체 A(우리 모델의 임베딩 분포)가 있습니다. 우리는 이 물체 A가 완벽한 '구(球)' 모양인 물체 B(이상적인 가우시안 분포)와 똑같은 모양인지 확인하고 싶습니다. 하지만 3차원 공간을 한 번에 비교하는 것은 너무 어렵습니다.
* **크라메르-볼트 정리의 해법:**
> "만약 당신이 **가능한 모든 방향**에서 손전등을 비춰서 벽에 생긴 물체 A의 2차원 '그림자'를 확인했을 때, 그 그림자가 **항상** 완벽한 '원(圓)' 모양(물체 B의 그림자)이라면, 당신은 원래의 3D 물체 A가 완벽한 '구(球)' 모양이라고 100% 확신할 수 있다."
이 정리는 2D/3D뿐만 아니라, **모든 고차원(K-dimension)**에 대해 성립합니다.
**즉, 어떤 고차원 확률 분포는, 그것의 모든 가능한 1차원 프로젝션(그림자)들의 집합에 의해 유일하게 결정됩니다.**
---
### LeJEPA의 전략: 1차원 정리와 고차원 정리를 결합하다
LeJEPA는 이 두 가지 강력한 수학적 정리를 아름답게 결합하여 사용합니다.
1. **목표 설정:**
* 우리의 최종 목표는 K-차원의 임베딩 분포(`P_θ`)를 K-차원의 **등방성 가우시안 분포(`Q_target`)** 와 똑같이 만드는 것입니다.
2. **문제 분해 (크라메르-볼트 정리 적용):**
* K-차원에서 직접 비교하는 것은 불가능하니, 문제를 수많은 1차원 문제로 분해합니다.
* "모든 가능한 1차원 방향 `a`에 대해, `P_θ`를 `a`에 프로젝션한 1차원 분포(`P_θ^(a)`)가 `Q_target`을 `a`에 프로젝션한 1차원 분포(`Q_target^(a)`)와 같아지도록 만들자."
* (여기서 아주 좋은 점은, `Q_target`이 등방성 가우시안이면, 그것의 1차원 프로젝션 `Q_target^(a)`는 어떤 방향 `a`에 대해서든 **항상 똑같은 모양의 표준 정규분포**가 된다는 것입니다.)
3. **1차원 문제 해결 (특성 함수의 유일성 정리 적용):**
* 이제 우리는 `P_θ^(a)` 와 `표준 정규분포`라는 두 개의 **1차원 분포**를 비교하는 단순한 문제만 풀면 됩니다.
* 바로 이 지점에서 Epps-Pulley 테스트가 등장합니다. Epps-Pulley는 두 1차원 분포의 **특성 함수(지문)**를 비교합니다.
* 사용자님께서 말씀하신 "특성 함수의 유일성 정리"에 따라, 만약 두 1차원 분포의 특성 함수가 같다면, 그 두 1차원 분포는 완전히 동일합니다.
### LeJEPA의 전체 논리 흐름
**만약** → Epps-Pulley 손실이 0이 되어서,
**모든 방향 `a`에 대해** → 우리 임베딩의 1차원 '그림자'(`P_θ^(a)`)의 특성 함수가,
표준 정규분포의 특성 함수와 같아진다면,
**(특성 함수의 유일성 정리에 의해)**
**그러면** → **모든 방향 `a`에 대해** → 우리 임베딩의 1차원 '그림자'(`P_θ^(a)`) 자체가
표준 정규분포와 같아진다는 뜻이고,
**(크라메르-볼트 정리에 의해)**
**그러면** → 원래의 K-차원 임베딩 분포(`P_θ`) 자체가
K-차원 등방성 가우시안 분포(`Q_target`)와 같아진다는 것이 **수학적으로 보장됩니다.**
---
**실용적 측면 (현실과의 타협):**
물론 실제 코드에서는 '모든' 방향(무한대)을 다 확인할 수는 없습니다. 그래서 LeJEPA는 두 가지 현실적인 타협을 합니다.
1. **샘플링:** 매 학습 스텝마다, '모든' 방향 대신 `M`개의 **무작위 방향을 샘플링**하여 확인합니다.
2. **누적 효과:** 이 과정을 수십만 번 반복하면, 전체 학습 과정 동안 **사실상 거의 모든 방향을 다 훑어보는 누적 효과**가 발생하여, 이론적인 보장에 매우 가깝게 근사할 수 있습니다.