[최적화] (3) 모멘텀과 SGD / Momentum 수학적 정의 / Adagrad와 차이

모멘텀(Momentum) ?

확률적 경사 하강법(SGD, Stochastic Gradient Descent)에 가속도 항을 추가하여 기울기의 관성 효과를 반영하는 최적화 기법.

SGD의 단점을 보완하고 더 빠르고 안정적으로 최적점에 도달할 수 있게 한다.

모멘텀의 원리

이전 단계의 기울기 업데이트를 일정 부분 기억하여 현재 단계의 업데이트에 반영하는 것.

이를 통해 최적화 과정에서 기울기의 변동을 완화하고 더 빠르게 수렴할 수 있다.

모멘텀은 물리학에서의 운동량과 유사한 개념으로, 관성을 활용하여 최적화 경로를 더 부드럽고 효율적으로 만들어준다.

---

수학적 정의

모멘텀을 적용한 SGD의 업데이트 방식 :

1. 모멘텀 항 업데이트 : 
   • v_t : 현재 모멘텀 값
   • gamma : 모멘텀 계수, 일반적으로 0.9 정도로 설정
   • η : 학습률
   • ∇L(θ_t) : 현재 가중치 θ_t에서의 손실 함수 L의 기울기

2. 파라미터 업데이트:
θt+1=θt−vt
모멘텀 항 v_t는 이전 단계의 모멘텀 v_{t-1}에 현재 기울기 ∇L(θt)를 더한 값.
이 값을 이용하여 파라미터 θ를 업데이트

---

모멘텀의 효과

1. 가속도: 최적화 과정에서 기울기가 일정한 방향으로 계속되는 경우, 모멘텀 항은 가속도를 부여하여 더 빠르게 수렴할 수 있도록 돕는다. 특히 볼록(convex) 함수의 최적화에서 효과적이다.
2. 진동 완화: 모멘텀은 최적점 주변에서 발생할 수 있는 진동을 완화하는 데 도움이 된다. 이는 기울기가 자주 변하는 경우에도 안정적인 학습을 가능하게 한다.
3. 지역 최적점 탈출: 모멘텀은 파라미터가 지역 최적점에 갇히는 것을 방지하고 더 나은 전역 최적점을 찾는 데 도움을 준다.

---

모멘텀과 표준 SGD 비교

• 표준 SGD:

• 표준 SGD는 현재 기울기만을 사용하여 파라미터를 업데이트.
• 모멘텀을 적용한 SGD:

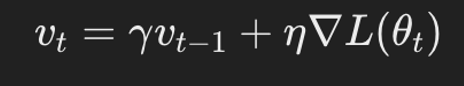
모멘텀을 적용한 SGD는 이전 단계의 업데이트 방향을 반영하여 보다 부드럽고 효율적인 학습 경로를 제공.

→

모멘텀은 SGD에 관성 효과를 추가함으로써 최적화 속도를 높이고 진동을 줄이며, 더 안정적이고 효율적인 학습을 가능하게 한다.

---

모멘텀과 Adagrad 차이

• 목표:
  • 모멘텀: 경사하강법의 경로를 부드럽게 하고, 진동을 줄이며, 더 빠르게 수렴할 수 있도록 돕는 것이 목표
  • Adagrad: 학습률을 각 파라미터마다 다르게 조정하여 자주 등장하는 특징과 자주 등장하지 않는 특징을 균형 있게 학습하는 것이 목표
• 방법:
  • 모멘텀: 이전 기울기의 영향을 현재 업데이트에 반영하여 경사하강법에 가속도를 부여.
  • Adagrad: 기울기 제곱의 누적합을 사용하여 학습률을 조정
  •  

---

다른게시물 참고바람

https://minsunstudio.tistory.com/36

https://minsunstudio.tistory.com/33

[이론헷갈리지마] 경사하강법, 확률적 경사하강법 SGD stochastic Gradient discent