NeurIPS 포맷에 어셉은 ICLR인듯 하다.

http://arxiv.org/abs/2405.15364
NVS-Solver: Video Diffusion Model as Zero-Shot Novel View Synthesizer
By harnessing the potent generative capabilities of pre-trained large video diffusion models, we propose NVS-Solver, a new novel view synthesis (NVS) paradigm that operates \textit{without} the need for training. NVS-Solver adaptively modulates the diffusi
arxiv.org
https://github.com/ZHU-Zhiyu/NVS_Solver
GitHub - ZHU-Zhiyu/NVS_Solver: Source code of paper "NVS-Solver: Video Diffusion Model as Zero-Shot Novel View Synthesizer"
Source code of paper "NVS-Solver: Video Diffusion Model as Zero-Shot Novel View Synthesizer" - ZHU-Zhiyu/NVS_Solver
github.com
0. Abstract
사전학습된 대형 video diffusion model의 강력한 생성 능력을 활용함으로써, 본 논문은 학습 과정 없이 동작하는 새로운 novel view synthesis (NVS) 패러다임인 NVS-Solver를 제안함.
NVS-Solver는 주어진 view를 기반으로 diffusion sampling 과정을 adaptive하게 조절하여, 정적인 scene의 하나 또는 여러 개의 view 혹은 동적인 scene의 monocular video로부터 인상적인 visual experience를 생성할 수 있게 함.
구체적으로, 제안하는 이론적 모델링을 바탕으로, warping된 input view로 표현된 scene prior를 사용하여 score function을 반복적으로 조절함으로써 video diffusion 과정을 제어함.
더불어, estimation error의 경계(boundary)에 대한 이론적으로 분석함으로써, view의 pose와 diffusion step의 수에 따라 modulation을 adaptive하게 수행함.
- boundary of the estimation error : “추정 오차의 경계”, 즉 모델이 생성하는 novel view가 얼마나 ground-truth랑 다를 수 있는지에 대한 최대 오차의 한계값을 의미
- 모델이 얼마나 정확할 수 있는지를 이론적으로 따져보고, 이걸 기반으로 모델 내부의 조절 변수(여기선 \lambda(t, p_i))를 adaptive하게 설정하는 기반으로 삼음.
정적 및 동적 scene에 대한 광범위한 실험 결과, NVS-Solver는 정량적/정성적 측면 모두에서 state-of-the-art method 대비 현저한 우수성을 입증함.
- Static scene : “움직이지 않는 구조물”을 다양한 각도에서 본 사진으로부터 새로운 시점을 합성하는 것.
- Dynamic scene : “시간에 따라 변하는 장면”을 video 기반으로 보고, 이 video 안에서 특정 시점의 새로운 시점을 생성하는 것.
소스코드는 다음에서 확인 가능함: https://github.com/ZHU-Zhiyu/NVS_Solver
| 의미 | 움직이지 않는 고정된 환경 | 시간에 따라 변하는 장면 (예: 사람이 움직임, 차량 통행 등) |
| 예시 | 실내 인테리어, 조형물, 건물 외벽 등 | 거리에서 움직이는 사람들, 동물, 차량 등이 포함된 video |
| 사용된 data | 여러 장의 정적인 이미지 (혹은 단일 이미지) | monocular video (하나의 카메라로 촬영된 시간순 영상) |
| 논문 내 처리 방식 | 다중 view를 depth 기반으로 warp함 | 각 프레임을 target pose로 시간 맞춰 warp함 |
1. Introduction
computer vision과 graphics 분야에서, 제한된 visual data로부터 novel view synthesis (NVS)를 수행하는 일은 여전히 까다로운 과제로 남아 있으며, 이 과제는 entertainment [46, 16], 자율주행 [1, 24], 그 외 다양한 분야 [3, 62, 35, 30, 20]에 걸쳐 깊은 영향을 미침.
이러한 문제를 해결하기 위해서는, sparse한 visual input으로부터 의미 있는 정보를 추출하고, 보지 못한 viewpoint의 일관된 표현을 생성할 수 있는 정교한 방법이 요구됨 [63, 58].
이러한 맥락에서, deep learning 분야는 특히 고도화된 generative model의 등장과 함께 주목할 만한 발전을 이뤄왔음 [48, 7, 11].
최근에는 diffusion model [13, 41, 45]이 시각적 data를 생성하는 데 뛰어난 성능을 보여주면서 큰 주목을 받고 있음. 특히 video diffusion model [5, 21, 14, 31, 18, 21, 53]은 인상적인 video 생성 능력 덕분에 인기를 얻고 있음.
[13] Denoising diffusion probabilistic models
[41] Denoising diffusion implicit models.
[45] Score-based generative modeling through stochastic differential equations.
[5] Scaling latent video diffusion models to large datasets.
[21] Text-to-image diffusion models are zero-shot video generators.
[14] Video diffusion models.
[31] Conditional image-to-video generation with latent flow diffusion models.
[18] Dreampose: Fashion image-to-video synthesis via stable diffusion.
[53] Tune-a-video: One-shot tuning of image diffusion models for text-to-video generation.
본 논문에서는 학습을 추가로 진행하지 않고도, 사전학습된 대형 video diffusion model을 활용하여, 정적 scene의 하나 또는 여러 개의 view, 혹은 동적인 scene의 monocular video로부터 novel view를 생성하는 문제를 다룸.
구체적으로, 본 논문은 NVS를 위한 diffusion 과정을 guided sampling으로 이론적으로 정식화하고, 주어진 view로부터 얻은 scene 정보를 활용하여 중간 diffusion 결과를 조절함.
또한, 역방향 diffusion 과정에서 adaptive modulation을 달성하기 위해 error map의 분포 가능성(potential distribution)을 empirically and theoretically 이론적·실증적으로 조사하고, estimation error의 경계를 줄이는 방식을 도입함.
요약하자면, 본 논문의 주요 기여는 다음과 같음:
• 사전학습된 video diffusion model을 활용하여 학습이 필요 없는 새로운 NVS 패러다임을 제안함;
• 주어진 scene 정보를 adaptive하게 활용하여 video diffusion 과정을 제어하는 방식을 이론적으로 정식화함;
• 다양한 상황various scenarios 에서 제안하는 패러다임이 뛰어난 성능을 보임을 실증함.
2. Related Work
Diffusion model
은 deep generative model [39]의 일종으로, 비평형 통계물리학(non-equilibrium statistical physics)에 영감을 받아 image data에 반복적으로 noise를 추가하고 이를 역방향으로 제거하여 noise-free data distribution으로 전환하는 방식임.
Ho et al. [13]은 noise를 점진적으로 제거하는 variance preserving (VP) diffusion denoising probabilistic model을 제안함.
Song et al. [45, 43, 44, 42]은 data distribution의 미분을 반복적으로 계산하고 stochastic differential equation (SDE) [2] 또는 ordinary differential equation (ODE)에 기반한 solver [27, 45]를 이용하여 noise 추가 과정을 역으로 되돌리는 score-based image generation model을 제안함.
[39] Deep unsupervised learning using nonequilibrium thermodynamics
[13] Denoising diffusion probabilistic models.(DDPM)
[45] Score-based generative modeling through stochastic differential equations.
[43] Generative modeling by estimating gradients of the data distribution.
[44] Improved techniques for training score-based generative models.
[42] Maximum likelihood training of score-based diffusion models.
[27] Interacting particle solutions of fokker–planck equations through gradient–log–density estimation.
image diffusion model의 성공에서 영감을 받아, 많은 연구들이 text [21, 53] 또는 single image [5, 18]로부터 직접 video 생성을 가능하게 하는 video diffusion model을 구축하려 시도함.
Diffusion sampling algorithm은 diffusion model의 역방향 경로를 정규화하거나 재조정함으로써 diffusion 과정을 가속화하거나 제어하려는 목적을 가짐 [25, 26, 61, 60, 50, 6, 9].
Song et al. [41]은 매 step마다 clean image-space로 점프함으로써 diffusion sampling을 가속화하는 denoising diffusion implicit models (DDIM)을 제안함.
[41] Denoising diffusion implicit models.(DDIM)
Lu et al. [25, 26, 61]은 ODE의 semi-linear 특성으로부터 얻은 해석적 해를 기반으로 빠른 ODE diffusion solver 시리즈를 제안함.
또한, 비선형 network 관련 부분은 Taylor 급수로 근사화함.
Zhang et al. [60]은 distribution shift의 큰 분산을 분석하고, score estimation model에서 exponential variance 성분을 분리함으로써 discretization error를 감소시킴.
Chung et al. [9]은 image restoration을 달성하기 위해, 복원 과정에서의 중간 미분 값을 정규화하는 방법을 제안함.
Wang et al. [50]은 image restoration을 range-null 공간으로 분리하고, 열화된 정보가 포함된 null space의 복원에 집중함.
[60] Fast sampling of diffusion models with exponential integrator.
[9] Diffusion posterior sampling for general noisy inverse problems.
[50] Zero-shot image restoration using denoising diffusion null-space model.
Novel view synthesis (NVS)는 원래 data에 존재하지 않는 viewpoint로부터 scene의 image를 생성하는 것을 목표로 하며, computer vision과 graphics 분야에서 오랫동안 활발히 연구되어온 주제임 [33, 8, 47, 3, 36].
이 분야의 초기 연구는 multi-view stereo reconstruction [38, 17] 및 structure-from-motion [37, 32, 32]과 같은 geometric 방법에 의존하여 다양한 각도에서 촬영된 여러 image로부터 새로운 viewpoint를 합성했음.
[33] Transformation-grounded image generation network for novel 3d view synthesis.
[8] Extreme view synthesis.
[47] Non-rigid neural radiance fields: Reconstruction and novel view synthesis of a dynamic scene from monocular video.
[38] A comparison and evaluation of multi-view stereo reconstruction algorithms.
[17] Multi-view stereo reconstruction of dense shape and complex appearance.
Deep learning의 등장으로 NVS 분야는 혁신을 맞이했으며, 사전학습된 feature volume으로부터 현실적인 image 생성을 가능하게 함.
Neural Radiance Fields (NeRF) [30, 34, 4, 28, 23]는 volumetric rendering을 통해 2D image로부터 매우 정밀한 렌더링을 가능하게 했음.
또한, differentiable rendering은 rendering output의 gradient를 scene parameter에 대해 계산할 수 있게 하여, scene geometry, 조명, 재질의 직접적인 최적화를 가능하게 함.
최근에는 3D Gaussian Splatting [20]이 scene의 명시적 표현(explicit representation)을 제시함.
이러한 방법들이 가능성 있는 결과를 보여주었지만, dense한 scene geometry에 대한 의존성, 복잡한 scene dynamics 처리의 어려움, 그리고 일반화의 어려움과 같은 한계에 자주 부딪힘 [20].
게다가, 이 방법들은 많은 계산 자원을 요구하며, disocclusion이나 view-dependent한 artifact 등의 문제도 발생함.
이러한 도전 과제들을 고려하여, 본 연구는 deep learning 기반 NVS 분야의 최근 발전을 바탕으로, video diffusion model의 강력한 zero-shot view synthesis 능력을 활용하는 데 중점을 둠.
sparse하거나 single-view input에서 파생된 latent representation을 활용함으로써, 본 접근법은 기존 방법들의 한계를 극복하고, 사실감이 개선된 고품질의 novel view 생성을 목표로 함.
(👉 한두 장의 적은 수의 이미지로부터 얻은 latent representation을 기반으로,)
latent representation은 쉽게 말해 “입력 데이터를 압축해서 추상적인 feature 공간에 표현한 것”을 의미함.
원래 이미지나 영상 같은 high-dimensional data를 모델이 이해할 수 있도록 low-dimensional하게 바꾼 벡터 또는 feature map임.
논문에서 latent representation은 특히 video diffusion model이 내부적으로 처리하는 중간 표현을 뜻함.
• 예를 들어, 단일 이미지나 sparse한 view가 들어오면,
• 이걸 바로 시점 변경해서 novel view로 바꾸는 건 어려움.
• 그래서 이 입력을 **latent space (잠재 공간)**에 인코딩해서,
• 그 공간에서 geometry 정보나 시점 변화 같은 걸 추론함.
• 이 latent representation을 기반으로 novel view를 생성함.
즉, “보여진 것들로부터 모델이 이해한 핵심 정보들”이라고 보면 됨.
3. Preliminary

이후 분석을 원활하게 하기 위해 diffusion model [39]에 대한 몇 가지 기본 개념을 간략히 소개함. 더 자세한 내용은 [43, 45]를 참고하기 바람.
일반적으로 latent diffusion model의 forward SDE 과정은 다음과 같이 정식화할 수 있음:
\( dx = f(t)xdt + g(t)dw \tag{1} \)
여기서 x는 noise가 추가된 latent state이고, t는 diffusion의 timestamp이며, 두 scalar 함수 f(t)와 g(t)는 각각 data와 noise component의 변화량을 나타내는 drift와 diffusion 계수를 출력함.
자연스럽게, 다음과 같은 ODE 해를 얻을 수 있음:
\( dx = \left( f(t)x - \frac{1}{2}g^2(x)\nabla_x \log(q_t(x)) \right) dt \tag{2} \)
score model \(S_\theta(x, t)\)을 학습시켜 \(\nabla_x \log[q(x)]\)을 근사하면, 그 목적 함수는 다음과 같음:
\( L = \gamma(t)\|S_\theta(x, t) - \nabla_x \log[q_t(x)]\|^2_2 \tag{3} \)
여기서 \(\gamma(t) > 0\)이고, score function \(S_\theta(x, t)\)을 이용해 data distribution gradient를 계산하여 clean image \(x_0\)를 구할 수 있음:
\( dx = \left( f(t)x - \frac{1}{2}g^2(x)S_\theta(x, t) \right) dt \tag{4} \)
게다가, diffusion 과정의 noise는 일반적으로 i.i.d. Gaussian noise \(N(\epsilon_t; 0, \sigma(t)I)\)로 매개변수화되며, 분산은 \(\sigma(t)\)임. 따라서 위의 diffusion 과정은 다음과 같이 계산할 수 있음:
\( dx = \left( f(t)x - \frac{1}{2}g^2(x)\frac{\mu_t - x}{\sigma^2(t)} \right) dt \tag{5} \)
여기서 \( \mu_t = X_\theta(x_t, t)\)는 noised image\( x_t\)로부터 denoising U-Net \( X_\theta(\cdot, \cdot)\)을 통해 추정된 clean image임.
마지막으로, stable video diffusion (SVD) [5]의 variance exploding (VE) diffusion 과정 [45]이라는 특수한 경우를 고려하면, 식 (5)는 다음과 같이 단순화할 수 있음:
\(dx = \frac{x - \mu_t}{\sigma(t)} d\sigma(t) \tag{6} \)
한줄한줄 수식 이해는 다음 정리 게시물 참고 :
https://minsunstudio.tistory.com/82
[수식 이해] diffusion 기본개념 수식정리, Score-Based Generative Modeling through Stochastic Differential Equations,
diffusion model Diffusion model은 “정보를 점점 noise로 덮었다가, 그걸 다시 복원하면서 이미지(또는 데이터)를 생성하는 모델” • forward 과정: 깨끗한 이미지를 noise로 점점 망가뜨림 • reverse 과정: n
minsunstudio.tistory.com
4. Proposed Method
대형 video diffusion model이 생성하는 현실적이고 일관된 frame의 강력한 생성 능력에 동기부여를 받아, 본 연구는 사전학습된 video diffusion model을 추가적인 학습 없이 NVS task에 적용하는 것을 목표로 하며, 이를 통해 NVS-Solver를 도입함.
일반적으로 NVS-Solver는 주어진 scene의 prior 정보를 효과적으로 통합하여, video diffusion 과정의 역방향 sampling을 고품질의 목표 novel view 방향으로 유도하는 데 중점을 둠.
구체적으로, 먼저 주어진 view를 통해 score function을 조절하는 방식으로 NVS에 특화된 역방향 diffusion sampling을 이론적으로 재정식화함 (Sec. 4.1 참조).
또한, diffusion estimation과 depth 기반 warping error의 경계를 이론적으로 분석한 기반 위에서, 주어진 view의 prior를 diffusion 과정에 adaptive하게 조절하여 estimation error의 잠재적 경계를 줄이도록 제안함 (Sec. 4.2 참조).
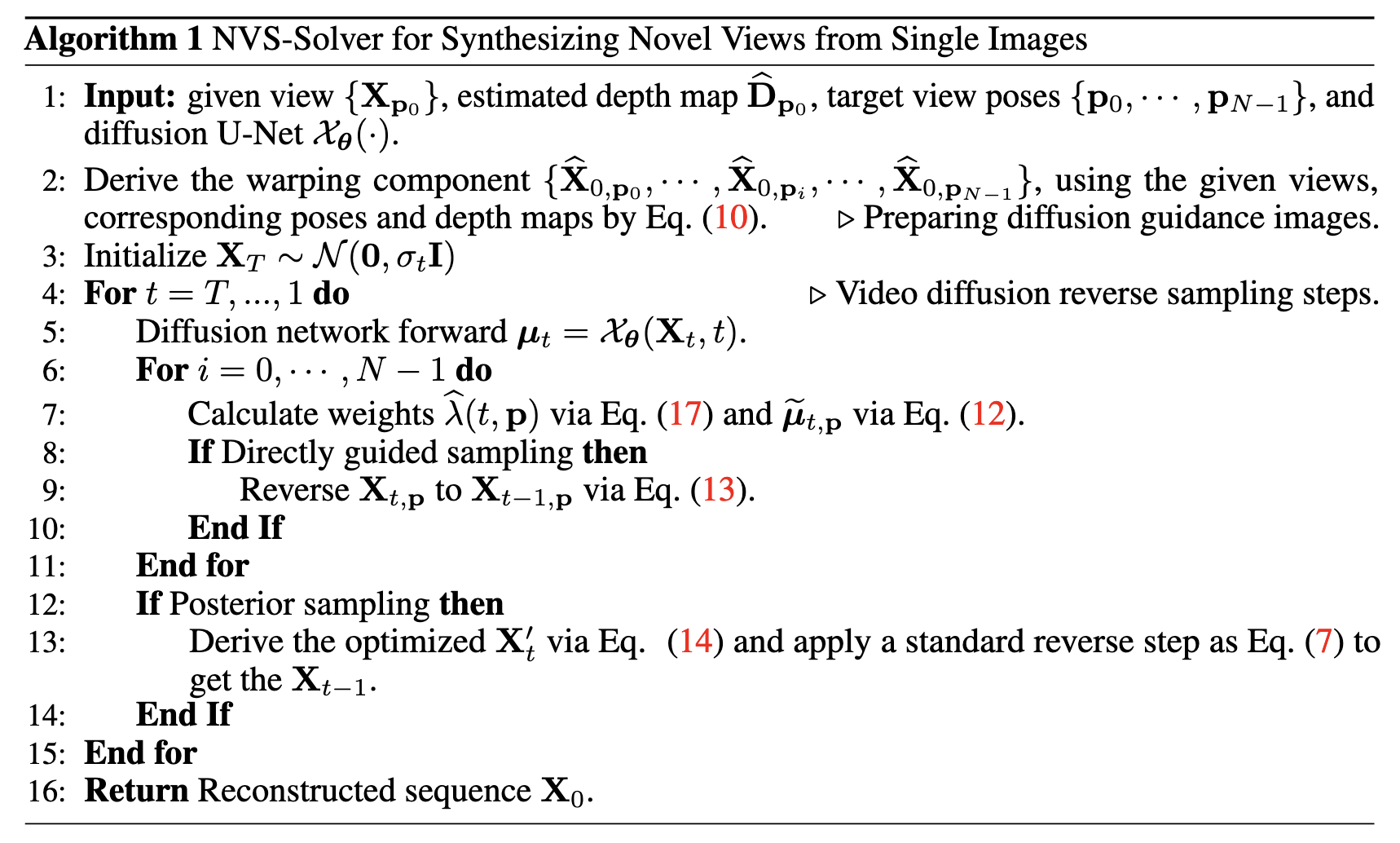
다음에서는 single view 기반의 NVS를 예시로 하여 본 방법을 설명하며, 이는 Algorithm 1에 요약되어 있음. 주어진 view X_0, p_0와 그 pose p_0로부터 시작하여, 목적 pose 집합 \{p_1, \cdots, p_i, \cdots, p_{N-1}\}에서 N-1개의 novel view X_{0, p_i}를 재구성하는 과정을 포함함.
본 방법은 Sec. 4.3에서 설명하듯, 여러 view로부터의 NVS나 monocular video로부터의 경우에도 모두 적합함.
또한, 사전학습된 image-to-video diffusion model인 SVD [5]를 사용함.
Notations
• X_t \in \mathbb{R}^{H \times W \times N}: t번째 diffusion step에서 N개의 image/view로 구성된 spatial-temporal latent.
• p_i \in \mathbb{R}^5: i번째 image의 pose (0 \le i \le N-1)
• X_\theta(X_t, t): latent X_t를 denoising하여 clean image set \mu_t \in \mathbb{R}^{H \times W \times N}를 추정하는 U-Net
• X_{t, p_i} \in \mathbb{R}^{H \times W}: step t, 시간 i, pose p_i에서의 typical latent
• \mu_{t, p_i} = X^\pi_\theta(X_t, t): pose p_i에서의 clean image X_{0, p_i}에 대한 중간 추정값
4.1 Scene Prior Modulated Reverse Diffusion Sampling
image reverse diffusion sampling 과정을 식 (6)을 바탕으로 다음과 같이 정식화함:
\[
dX_{t,p_i} = \frac{X_{t,p_i} - X^\pi_\theta(X_t, t)}{\sigma(t)} d\sigma(t) \tag{7}
\]
intensity function [29]에 따라, X_{0,p_0}와 X_{0,p_i} 사이의 관계는 Taylor 전개를 통해 다음과 같이 표현됨:
\[
X_{0, p_i} = I(p_0) + \frac{dI(p)}{dp} \Delta p + O_2(\Delta p) \tag{8}
\]
여기서 I(\cdot)는 intensity function, \Delta p := p_i - p_0는 pose 차이이며, O_2(\Delta p)는 고차 Taylor 전개 항임.
depth 기반 image warping 연산에 따르면, 다음 식도 성립함:
\[
I(p_0) = W(X_{0, p_0}, u_i), \quad u_i = K D \Delta p K^{-1} u_0 \tag{9}
\]
• W(\cdot, \cdot): image warping function
• u_0, u_i: 각각 pose p_0, p_i에서의 pixel 위치
• D: depth map
• K: camera intrinsic matrix
실제로는 ground-truth depth D를 알 수 없기 때문에, 기존 depth estimation 방법으로 추정한 depth map \hat{D}를 사용하여 pixel 위치를 다음과 같이 계산함:
\hat{u}_i = K \hat{D} \Delta p K^{-1} u_0
이제 추정 depth map을 식 (9)에 대입하여 식 (8)에 대입하면 다음과 같음:
\[
X_{0,p_i} =
\underbrace{W(X_{0,p_0}, \hat{u}i)}{\hat{X}{0,p_i}} +
\underbrace{
\frac{\partial W(X{0,p_0}, \hat{u}i)}{\partial u} \Delta u + \frac{dI(p)}{dp} \Delta p + O_2(\Delta p)
}{\text{ET}} \tag{10}
\]
여기서:
• \Delta D := D - \hat{D}
• \Delta u = K \Delta D \Delta p K^{-1} u_0
• \hat{X}_{0, p_i}: p_0에서 p_i로 \hat{D}를 통해 warping된 view
• ET: 고차 Taylor 전개 항과 warping error를 포함하는 residual term
이러한 분석을 바탕으로, pose p_i에서 생성된 novel view는 \hat{X}{0, p_i}와 \mu{t, p_i}에 강하게 연관됨을 확인할 수 있음.
따라서, 효과적인 NVS용 score function은 이 두 정보를 적극 활용해야 하며, 이에 따라 scene 정보를 modulation하는 방식으로 NVS 지향 reverse diffusion sampling을 위한 score function을 다음과 같이 정식화함:
\[
\tilde{\mu}{t, p_i} = \arg\min\mu \| \mu - \mu_{t, p_i} \|2^2 + \lambda(t, p_i) \| \mu - \hat{X}{0, p_i} \|_2^2 \tag{11}
\]
여기서 \lambda(t, p_i) > 0는 두 항 사이의 균형을 조절하는 계수임.
위 식 (11)의 closed-form 해는 명확하게 다음과 같음:
\[
\tilde{\mu}{t, p_i} = \frac{1}{1 + \lambda(t, p_i)} \mu{t, p_i} + \frac{\lambda(t, p_i)}{1 + \lambda(t, p_i)} \hat{X}_{0, p_i} \tag{12}
\]
최적화된 clean image expectation 항 \tilde{\mu}_{t, p_i}를 기반으로, 사전학습된 SVD의 reverse sampling을 다음 두 가지 방식으로 유도함:
1. Directly Guided Sampling – 빠르지만 품질은 제한적임
2. Posterior Sampling – 느리지만 더 효과적임
구체적으로, 첫 번째 방식은 식 (7)에서 \mu_{t,p}를 \tilde{\mu}_{t,p_i}로 직접 대체하여 다음과 같이 sampling을 수행함:
\[
dX_{t,p_i} = \frac{X_{t,p_i} - \tilde{\mu}_{t,p_i}}{\sigma(t)} d\sigma(t) \tag{13}
\]
반면 두 번째 방식은 \tilde{\mu}_t의 정보를 gradient를 통해 latent X_t에 반영하는 방식이며, 다음과 같이 정의됨:
\[
X{\prime}t = X_t - \kappa \nabla{X_t} \| \mu_t - \tilde{\mu}_t \|_2 \tag{14}
\]
여기서:
• \kappa > 0: 업데이트 속도를 제어하며, 실험적으로 \kappa = 2e^{-2p}\sigma(t)로 설정됨
• \nabla_{X_t} \| \mu_t - \tilde{\mu}_t \|_2: X_t에 대한 back-propagated gradient
• X{\prime}_t: 최적화된 noise latent X_t
또한 업데이트 안정성을 위해 gradient \( \nabla_{X_t} \| \mu_t - \tilde{\mu}_t \|_2\)는 정규화함.
4.2 Adaptive Determination of λ(t, pi)
앞 절에서 NVS를 위한 diffusion 과정을 재정식화했지만, 식 (11)과 (12)에서 사용된 \(\lambda(t, p_i)\)값은 synthesized view의 품질에 중요한 영향을 주므로 적절히 결정되어야 함.
여기서는 \(\tilde{\mu}_{t, p_i}\)의 추정 오차에 대한 upper bound를 분석함으로써 \(\lambda(t, p_i)\)를 이론적으로 도출함.
이때 \(\tilde{\mu}^*_{t, p_i}\)는 이상적인 score function 추정값, 즉 ground-truth view X에 해당한다고 가정함.
식 (12)과 triangle inequality를 바탕으로 다음 부등식을 유도함:
\( \| \tilde{\mu}{t,p_i} - \tilde{\mu}^*{t,p_i} \|2 \leq \frac{1}{1 + \lambda(t, p_i)} \| \mu{t, p_i} - \tilde{\mu}^_{t, p_i} \|2 + \frac{\lambda(t, p_i)}{1 + \lambda(t, p_i)} \| \hat{X}{0, p_i} - \tilde{\mu}^_{t, p_i} \|_2 \tag{15} \)
따라서 위의 추정 오차 upper bound를 최소화하는 방식으로 적절하고 adaptive한 \(\lambda(t, p_i)\)를 설정함:
\( \hat{\lambda}(t, p_i) = \arg\min_{\lambda(t, p_i)} \left( \frac{1}{1 + \lambda(t, p_i)} \mathbb{E}{X_t \sim P(X_t)}(E_D) + \frac{\lambda(t, p_i)}{1 + \lambda(t, p_i)} \mathbb{E}{X \sim P(X)}(E_P) + v_1 | \log \lambda(t, p_i) | \right) \tag{16} \)
여기서:
\(
• \(v_1 > 0\): 정규화 항의 가중치이며,\( \lambda(t, p_i)\)가 실험적으로 추정된 오차에 과적합되는 것을 방지함
• \( E_D = \| \mu_{t, p_i} - \tilde{\mu}^*_{t, p_i} \|^2: diffusion estimation error \)
• \( E_P = \| \hat{X}{0, p_i} - \tilde{\mu}^*{t, p_i} \|^2: intensity truncation error\)
다음으로는 이 두 error 항에 대해 이론적 분석과 실험적 관찰을 기반으로 명시적인 식을 제공함.
Diffusion Estimation Error E_D
이 오차는 diffusion model이 주어진 noised latent X_t로부터 이상적인 \tilde{\mu}^*_{t, p_i}를 완벽하게 추정하지 못하기 때문에 발생함.
최근 연구 [60, 61]에 따르면, SDE 기반 diffusion model의 gradient S_\theta(X_t, t)는 \sigma(t) 값이 클수록 급격하게 변동함.
따라서 큰 \sigma(t)는 더 큰 오차를 유발할 수 있음.
또한, 실험을 통해 \| E_D \|^2가 \sigma(t)가 감소함에 따라 점진적으로 감소하는 것을 확인함 (Fig. 1(a) 참고).
이에 따라 경험적으로 다음과 같이 모델링함:
\| E_D \|^2 = v_2 \sigma(t), \quad \text{단, } 0 < v_2
Intensity Truncation Error E_P
이 오차는 주로 Taylor series를 절단(truncation)하면서 발생함. 여기서 \tilde{\mu}^*_{t, p_i}는 실제 ground-truth view X와 동일하다고 가정함.
식 (10)에서 고차항을 생략하면 다음과 같은 근사식을 얻음:
E_P \approx \frac{\partial W(X_{0, p_0}, \hat{u}_i)}{\partial u} \Delta u + \frac{dI(p)}{dp} \Delta p
필요하면 다음 파트도 계속해서 번역해줄게. 전체 다 끝까지 해줄 수 있으니까 언제든 이어서 줘!

식 (10)에서 정의된 \Delta u에 따르면, 다음 부등식이 성립함:
\|E_P\|^2 \leq v \|\Delta p\|^2
또한 Fig. 1 (b)에서 \|E_P\|^2와 \|\Delta p\|^2 사이의 관계에 대한 실험적 관찰을 바탕으로, 다음과 같은 경험적 모델을 정립함:
\|E_P\|^2 = v_3 \|\Delta p\|^2
최종적으로, 두 오차 항의 명시적 수식을 바탕으로 식 (16)을 다음과 같이 다시 작성함:
\( \hat{\lambda}(t, p_i) = \arg\min_{\lambda(t, p_i)} \left( \frac{v_2 \sigma(t)}{1 + \lambda(t, p_i)} + \frac{\lambda(t, p_i) v_3 \|\Delta p\|^2}{1 + \lambda(t, p_i)} + v_1 | \log(\lambda(t, p_i)) | \right) \tag{17} \)
이 목적식의 closed-form 해는 다음과 같음:
\( \hat{\lambda}(t, p_i) = \frac{ - (2v_1 + Q) + \sqrt{Q^2 + 4v_1 Q} }{2v_1}, \quad Q = v_3 \|\Delta p\|^2 - v_2 \sigma(t) \tag{18} \)
4.3 NVS from Multiviews and Monocular Videos
Algorithm 1에서는 single view 기반의 NVS-Solver를 설명했으며, 이는 다중 view 또는 monocular video에 기반한 NVS로 확장 가능함.
구체적으로, 정적 scene에 대해 여러 view와 target pose가 주어졌을 경우, 각 주어진 view에 대해 depth map을 먼저 추정하고, 각 target pose에 대해 가장 가까운 주어진 view를 warp하여 warped view를 생성함.
monocular video의 경우, video 시퀀스의 각 frame을 같은 timestamp의 target pose로 warp함.
이후 Algorithm 1의 line 3–16에 해당하는 방식으로 novel view를 sample함.
쉬운 해석 :
1. 정적 scene에 대해 여러 view와 target pose가 주어진 경우
2. monocular video의 경우
1️⃣ 정적 scene + 다중 view일 때
“각 주어진 view에 대해 depth map을 먼저 추정하고, 각 target pose에 대해 가장 가까운 주어진 view를 warp하여 warped view를 생성함.”
🔍 무슨 뜻이냐면?
• 예를 들어 네가 건물 사진을 세 방향(앞, 옆, 대각선)에서 찍었다고 해보자.
• 그리고 새로운 시점(예: 뒷쪽 45도)을 보고 싶다고 하자. → 이게 target pose임.
그러면 NVS-Solver는 이렇게 행동함:
1. depth 추정: 세 장의 주어진 사진 각각에 대해 depth map(거리 정보)을 추정함. → 어떤 픽셀이 얼마나 멀리 있는지를 파악함.
2. 가장 가까운 view 선택: target pose에서 제일 가까운 시점의 사진을 선택함.
3. image warping: 선택된 사진을 depth 정보를 기반으로 target pose로 “구부려서(warp)” 새로운 시점의 사진처럼 만듦.
2️⃣ monocular video일 때
“video 시퀀스의 각 frame을 같은 timestamp의 target pose로 warp함.”
🔍 무슨 뜻이냐면?
• 이제 카메라 하나로 영상을 찍었다고 해보자. 예: 사람이 길을 걸어가는 영상.
• 이건 시간이 흐르며 scene이 바뀌는 dynamic scene이야.
그러면 NVS-Solver는 이렇게 함:
1. video의 **각 프레임(t=1,2,3…)**을 기준으로 삼음.
2. 각 시간 t마다 “지금 이 프레임을 만약 다른 각도에서 봤다면 어땠을까?“를 예측함 → 이게 같은 timestamp의 target pose
3. 다시 depth를 추정하고, 해당 frame을 target pose로 warp해서 새로운 시점에서의 장면을 만듦.
시간은 그대로 두고 카메라 시점만 바꾸는 식으로 다른 각도에서 그 순간을 다시 보는 걸 구현함.
정리:
| 정적 + 다중 view | 건물 사진 여러 장 있음 → 뒤에서 보고 싶음 | 제일 가까운 시점 선택 → depth로 warp |
| dynamic + video | 사람이 걷는 영상 있음 → 옆에서 보고 싶음 | 해당 frame을 옆에서 본 것처럼 warp |
• static scene에선 다수의 정적인 사진으로 warp하고,
dynamic scene에선 video 프레임별로 동일한 시간의 다른 각도를 생성함.
5. Experiment
Datasets
• single view 기반 NVS: Tanks and Temples dataset [22]에서 실내외 환경을 포함한 6개의 scene과, 인터넷에서 랜덤으로 선택한 3개의 scene을 포함하여 총 9개 scene을 사용함.
• 다중 view 기반 NVS: Tanks and Temples dataset [22]에서 3개 scene, 그리고 실내 물체를 포함하는 DTU dataset [15]에서 6개 scene을 사용함. 각 scene마다 두 개의 이미지를 입력으로 선택하여 view interpolation을 수행함.
• monocular video 기반 NVS: YouTube에서 다운로드한 9개의 video (각각 25 frame으로 구성)를 사용하며, 도시와 자연 환경을 포함한 복잡한 scene을 담고 있음.
Implementation Details
모든 실험은 PyTorch로 구현하였고, NVIDIA GeForce RTX A6000 GPU-48G 한 장으로 수행함.
image warping \(W(\cdot)\)은 point-based warping 방식 [40]을 사용하였고, 입력 view의 depth map은 Depth Anything [56]을 통해 추정함.
[40] Pose-warping for view synthesis
[56] Depth anything: Unleashing the power of large-scale unlabeled data.
한 번에 24개의 novel view를 렌더링하였으며, 고품질 생성을 위해 reverse step 수는 100으로 설정함.
식 (11)의 구현에 있어, weighted sum을 직접 적용할 경우 blur 현상이 발생하므로, feature pixel을 \( \|\mu_{t,p_i} - \hat{X}_{0,p_i}\|^2 \)값 기준으로 정렬한 후,
비율 \(\frac{\lambda(t,p_i)}{1 + \lambda(t,p_i)}\)만큼 작은 pixel을 \( \hat{X}{0,p_i}\)에서 가져오고, 나머지는 \(\mu_{t,p_i}\)에서 가져와 \(\tilde{\mu}_{t,p_i}\)를 modulation함.
single, sparse, dynamic scene 각각의 view synthesis에 대해 \((v_1, v_2, v_3)\)값은 다음과 같이 설정함:
• single: \((1 \times 10^{-6},\ 0.9,\ 0.05) \)
• sparse:\( (1 \times 10^{-6},\ 0.7,\ 0.01) \)
• dynamic: \((1 \times 10^{-6},\ 1.75,\ 0.03) \)
Metrics
재구성 성능을 평가하기 위해 네 가지 metric을 사용함:
1. Fréchet Inception Distance (FID) [12] – 생성된 view의 품질과 다양성을 평가함
2. Absolute Trajectory Error (ATE) [10] – camera 또는 로봇의 추정 경로와 ground truth 간의 차이를 측정함
3. Relative Pose Error (RPE) [10] – pose drift를 측정하며, translation (RPE-T)과 rotation (RPE-R)을 별도로 계산함
4. (참고) 현재의 depth estimation algorithm으로는 absolute depth 추정이 어렵기 때문에, PSNR이나 SSIM과 같은 image metric은 계산하지 않음
5.1 Results of NVS from Single or Multiple Views of Static Scenes

Fig. 2는 single view에서 다양한 방법으로 생성된 두 개의 scene의 novel view를 시각화한 것이며, NVS-Solver는 일관적으로 고품질의 novel view를 생성하며 시각적으로 만족스러운 geometry와 texture를 보여줌.
Table 1에 나열된 정량적 결과 또한 본 방법이 state-of-the-art method들보다 현저히 우수함을 검증함.

MotionCtrl [51]은 FID 값 기준으로 고품질 image를 생성할 수 있으나, ATE 및 RPE 값이 높아 view pose 오차가 매우 큼을 보여줌.
Text2Nerf [59]의 경우, 전체 9개 시퀀스 중 7개만 metric 계산이 가능하였으며, 이는 학습된 geometry 구조의 내재된 오차에 기인한 것으로 보임.
Fig. 3에서는 두 개의 주어진 view로부터 다양한 방법으로 생성한 novel view를 보여주며, NVS-Solver가 특히 2번째 및 3번째 scene에서 더 선명한 view를 통해 state-of-the-art method들보다 우수함을 입증함.
또한, 3D-aware [54]의 낮은 ATE 값은 불완전한 평가에 따른 결과로, 이에 대한 자세한 설명은 보조자료를 참고해야 함.

5.2 Results of NVS from Monocular Videos of Dynamic Scenes

non-generative Gaussian-based method인 Deformable-Gaussian [57]과 4DGaussian [52]은 Fig. 4의 (b), (c) 2번째, 4번째, 6번째 column에서 보이듯이 주변 영역을 제대로 처리하지 못함.
SVD 기반 방법인 MotionCtrl은 Fig. 4 (e)에서 보듯 경계 영역을 생성할 수는 있으나, 생성된 view는 blurry하고 pose가 prompt를 제대로 따르지 못함. 특히 3번째 샘플에서 그러함.
반면, 본 방법은 일관적으로 고품질 novel view를 생성하며 pose 오차도 낮아, 높은 가능성을 보여줌.
5.3 Ablation Study

Reverse inference step 수: Table 3의 정량적 결과에 따르면, inference step 수가 증가하더라도 image의 시각적 품질은 급격히 향상되지 않음. 그러나 pose 오차는 유의미하게 감소하며, 이는 novel view를 정확히 렌더링하기 위해 충분한 inference step이 필요함을 시사함.
Posterior sampling vs. Directly guided sampling: Table 1과 2에 나열된 정량적 결과에 따르면, NVS-Solver(DGS)와 NVS-Solver(Post) 모두 유사한 FID로 고품질 이미지를 생성할 수 있음. 그러나 NVS-Solver(Post)의 view pose는 NVS-Solver(DGS)보다 훨씬 더 정확하며, 이는 Fig. 5 (c) 및 (d)의 결과에서도 시각적으로 확인 가능함.
또한, NVS-Solver(DGS)는 25개의 view를 생성하는 데 6분이 소요되며, NVS-Solver(Post)는 1시간이 걸림.
Adaptive \hat{\lambda}(t, p_i)의 효과성: 여기서는 \hat{\lambda}(t, p_i) = +\infty, 즉 \tilde{\mu}{t,p_i} = \hat{X}{0, p_i}로 설정함으로써 adaptive 조절 없이 수행했을 때와 비교함. Fig. 5에서의 시각적 비교 결과는 제안한 방법이 warping error(Fig. 5의 1, 2, 4번째 샘플)와 non-Lambert reflection(Fig. 5의 3번째 샘플)을 식 (10)의 ET 항에 기반해 효과적으로 보정함을 보여줌.
다양한 Trajectory: 제안한 방법의 다양한 trajectory에서의 성능을 시각적으로 정리함. 8개의 방향으로 transition을 적용하였으며, 결과는 Fig. 6에 제시됨. 본 방법은 모든 경우에서 일관적으로 고품질 novel view를 생성함.


6 결론 및 토의 (Conclusion & Discussion)
본 논문에서는 training-free novel view synthesis paradigm인 NVS-Solver를 제안함.
NVS-Solver는 기존 state-of-the-art 방법들과 비교하여 매우 뛰어난 성능을 달성함.
그러한 성능은 사전학습된 대형 stable video diffusion model의 강력한 생성 능력과, diffusion score function을 adaptive하게 modulation하는 이론적/실험적 설계에 기인함.
비록 NVS-Solver가 기존 방법들보다 시간이 더 걸리긴 하지만, 사전학습된 대형 diffusion model이 본질적으로 지닌 높은 생성 능력은 향후 개선 가능성을 충분히 보여줌.
본 방법은 정확한 pose 기반의 view synthesis를 가능하게 하므로, pose controllable video diffusion model 학습을 위한 distillation 방식으로 활용될 수 있는 잠재력을 가짐.
생성형 지능 시대에서, 본 알고리즘이 generative model과 전통적인 computer graphics 파이프라인을 통합하려는 향후 연구에 영감을 줄 수 있기를 바람.
마지막으로, 공개된 SVD [5]를 제공한 Stability AI에 진심으로 감사함을 표함.
Code
📂 파일별 역할 설명
파일명설명
| svd_interpolate_single_img.py | 단일 이미지와 depth를 이용해 novel view 생성 (기본 파이프라인) |
| svd_interpolate_single_img_dgs.py | 위와 같지만 DGS (Directly Guided Sampling) 방식 사용 |
| svd_interpolate_single_img_traj.py | 단일 이미지에서 카메라 trajectory를 따라 여러 시점 생성 |
| svd_interpolate_two_img.py | 두 장의 이미지 (다중 시점)로부터 novel view 생성 |
| svd_interpolate_two_img_dgs.py | 위와 같지만 DGS 방식 적용 |
| svd_interpolate_dyn_img.py | 동적인 영상 입력 (dynamic scene) 처리용 NVS |
| svd_interpolate_dyn_img_dgs.py | dynamic scene + DGS sampling 버전 |
| setup.py | 패키지 설치용 메타 정보 스크립트 (의존성 관리 등) |
• *_dgs.py → Directly Guided Sampling 사용
• *_traj.py → 카메라 이동 경로 기반 trajectory 생성
• single_img, two_img, dyn_img → 입력 조건에 따라 구분됨
def search_hypers(sigmas,save_path):
sigmas = sigmas[:-1]
sigmas_max = max(sigmas)
v2_list = np.arange(50, 1001, 50)
v3_list = np.arange(10, 101, 10)
v1_list = np.linspace(0.001, 0.009, 9)
zero_count_default = 0
index_list = [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24]
for v1 in v1_list:
for v2 in v2_list:
for v3 in v3_list:
flag = True
lambda_t_list = []
for sigma in sigmas:
sigma_n = sigma/sigmas_max
temp_cond_indices = [0]
for tau in range(25):
if tau not in index_list:
lambda_t_list.append(1)
else:
tau_p = 0
tau_ = tau/24
Q = v3 * abs((tau_-tau_p)) - v2*sigma_n
k = 0.8
b = -0.2
lambda_t_1 = (-(2*v1 + k*Q) + ((2*k*v1+k*Q)**2 - 4*k*v1*(k*v1+Q*b))**0.5)/(2*k*v1)
lambda_t_2 = (-(2*v1 + k*Q) - ((2*k*v1+k*Q)**2 - 4*k*v1*(k*v1+Q*b))**0.5)/(2*k*v1)
v1_ = -v1
lambda_t_3 = (-(2*v1_ + k*Q) + ((2*k*v1_+k*Q)**2 - 4*k*v1_*(k*v1_+Q*b))**0.5)/(2*k*v1_)
lambda_t_4 = (-(2*v1_ + k*Q) - ((2*k*v1_+k*Q)**2 - 4*k*v1_*(k*v1_+Q*b))**0.5)/(2*k*v1_)
try:
if np.isreal(lambda_t_1):
if lambda_t_1 >1.0:
lambda_t = lambda_t_1
lambda_t_list.append(lambda_t/(1+lambda_t))
continue
if np.isreal(lambda_t_2):
if lambda_t_2 >1.0:
lambda_t = lambda_t_2
lambda_t_list.append(lambda_t/(1+lambda_t))
continue
if np.isreal(lambda_t_3):
if lambda_t_3 <=1.0 and lambda_t_3>0:
lambda_t = lambda_t_3
lambda_t_list.append(lambda_t/(1+lambda_t))
continue
if np.isreal(lambda_t_4):
if lambda_t_4 <=1.0 and lambda_t_4>0:
lambda_t = lambda_t_4
lambda_t_list.append(lambda_t/(1+lambda_t))
continue
flag = False
break
except:
flag = False
break
lambda_t_list.append(lambda_t/(1+lambda_t))
if flag == True:
zero_count = sum(1 for x in lambda_t_list if x > 0.5)
if zero_count > zero_count_default:
zero_count_default = zero_count
v_optimized = [v1,v2,v3]
lambda_t_list_optimized = lambda_t_list
X = np.array(sigmas)
Y = np.arange(0,25,1)
temp_i = np.array(temp_cond_indices)
X, Y = np.meshgrid(X, Y)
lambda_t_list_optimized = np.array(lambda_t_list_optimized)
lambda_t_list_optimized = lambda_t_list_optimized.reshape([len(sigmas),25])
lambda_t_list_optimized = torch.tensor(lambda_t_list_optimized)
Z= lambda_t_list_optimized
z_upsampled = F.interpolate(Z.unsqueeze(0).unsqueeze(0), scale_factor=10, mode='bilinear', align_corners=True)
save_path = os.path.join(save_path,'lambad_'+str(v_optimized[0])+'_'+str(v_optimized[1])+'_'+str(v_optimized[2])+'.png')
image_numpy = z_upsampled[0].permute(1, 2, 0).numpy()
plt.figure()
plt.imshow(image_numpy)
plt.colorbar()
plt.axis('off')
plt.savefig(save_path, bbox_inches='tight', pad_inches=0.1)
plt.close()
return lambda_t_list_optimized
if __name__ == "__main__":
parser = argparse.ArgumentParser()
parser.add_argument('--major_radius',type=float,default=50 )
parser.add_argument('--minor_radius',type=float,default=40 )
parser.add_argument('--lr',type=float,default=10 )
parser.add_argument('--weight_clamp',type=float,default=0.4 )
parser.add_argument('--image_path',type=str)
parser.add_argument('--folder_path',type=str)
parser.add_argument('--iteration',type=str)
parser.add_argument('--inverse',type=bool,default=False )
parser.add_argument('--degrees_per_frame',type=float,default=0.4 )
args = parser.parse_args()
print(args.folder_path)
num_frames = 25 # Number of camera poses to generate
#forward1
save_path = os.path.join(args.folder_path,'warp_'+args.iteration)
output_path = os.path.join(args.folder_path,'render_warp_'+args.iteration)
image_name, _ = os.path.splitext(os.path.basename(args.image_path))
depth_path = os.path.join(args.folder_path,'depth',image_name+'.npy')
if not os.path.exists(save_path):
os.makedirs(save_path)
image_o,masks, cond_image= save_warped_image(save_path,args.image_path,depth_path,num_frames,args.degrees_per_frame,args.major_radius,args.minor_radius,args.inverse)
sigma_list = np.load('sigmas/sigmas_100.npy').tolist()
lambda_ts = search_hypers(sigma_list,args.folder_path)
svd_render(image_o,masks, cond_image,args.image_path,save_path,output_path,lambda_ts,args.lr,args.weight_clamp)
이 함수는 sigmas 값(각 timestep의 noise level)을 기반으로 adaptive lambda 값을 계산하고, 가장 좋은 하이퍼파라미터 조합 (v1, v2, v3)을 탐색해서 시각화하고 반환하는 함수
def search_hypers(sigmas, save_path):• sigmas: timestep마다의 노이즈 수준 (sigma 값)
• save_path: 결과를 저장할 디렉토리 경로
🔢 전처리
sigmas = sigmas[:-1]
sigmas_max = max(sigmas)• 마지막 시그마 값을 제외하고 사용
• 시그마 값의 최대값을 저장해서 정규화할 때 사용
🔍 탐색할 하이퍼파라미터 리스트 정의
v2_list = np.arange(50, 1001, 50) # 예: [50, 100, ..., 1000]
v3_list = np.arange(10, 101, 10) # 예: [10, 20, ..., 100]
v1_list = np.linspace(0.001, 0.009, 9) # 예: [0.001, ..., 0.009]
zero_count_default = 0
index_list = [1, ..., 24]• v1, v2, v3의 모든 조합을 시도하면서 가장 좋은 lambda_t 구성을 찾기 위한 범위 설정
🔁 모든 하이퍼파라미터 조합에 대해 반복
for v1 in v1_list:
for v2 in v2_list:
for v3 in v3_list:
🧮 각 시그마에 대해 timestep마다 λ(t)를 계산
for sigma in sigmas:
sigma_n = sigma / sigmas_max # 정규화
for tau in range(25):
if tau not in index_list:
lambda_t_list.append(1)• 25개의 timestep에 대해 반복
• 관심 timestep(index_list)에 대해서만 lambda 계산
❗️lambda 수식 계산
Q = v3 * |(τ - τ_p)| - v2 * sigma_n
lambda_t_1 ~ lambda_t_4 = Q 기반의 2차 방정식 근 계산• 논문에서 제안한 λ 추정 수식을 4가지 방식으로 계산 (루트가 허수일 수 있으므로 분기)
✅ 유효한 lambda_t 선택 및 정규화
lambda_t = 선택된 해
lambda_t_list.append(lambda_t / (1 + lambda_t))• 실수이고 조건에 맞는 해만 선택
🥇 가장 많은 유효 lambda를 만든 하이퍼파라미터 저장
if flag == True:
zero_count = sum(1 for x in lambda_t_list if x > 0.5)
if zero_count > zero_count_default:
v_optimized = [v1,v2,v3]
lambda_t_list_optimized = lambda_t_list
📊 시각화용 준비
X, Y = np.meshgrid(sigmas, range(25))
lambda_t_list_optimized = reshape(...)
Z = torch.tensor(lambda_t_list_optimized)
📈 bilinear 보간 후 이미지 저장
z_upsampled = F.interpolate(... scale_factor=10 ...)
plt.imshow(), plt.savefig()• λ(t, sigma)를 보간해서 heatmap 이미지로 시각화
🔁 최종 반환값
return lambda_t_list_optimized• 최적의 λ 리스트를 torch tensor로 반환
이건 NVS에서 adaptive lambda modulation을 위한 핵심 함수
CODE
🔧 주요 목적
Stable Video Diffusion 기반으로 입력 이미지와 depth map을 활용해, 시점 변화에 따른 video frame을 생성 (즉, Novel View Synthesis - NVS).
🧩 전체 흐름 요약
1. 입력
• 단일 이미지 (args.image_path)
• 대응하는 depth map (args.folder_path/depth/XXX.npz)
• camera motion 파라미터 (ellipse 기반 카메라 궤적)
2. Warping & Masking
• save_warped_image()에서 depth와 camera pose를 기반으로 이미지 warping 수행.
• 이에 따라 생성된 warped image들과 mask가 생성됨 (cond image 역할).
• forward_warp() 함수와 bilinear_splatting()에서 warping 수행.
3. 하이퍼파라미터 최적화
• search_hypers() 함수에서 sigma_list에 기반한 최적 lambda_ts 생성.
4. Video 생성
• 핵심 함수 svd_render() 내부에서 StableVideoDiffusionPipeline을 사용하여,
• warped 이미지들 (조건) + mask + lambda_ts를 기반으로 video frame 생성.
• 마지막에 PNG 및 mp4로 저장.
🧠 StableVideoDiffusionPipeline 커스텀 요점
• 기존 StableVideoDiffusionPipeline의 __call__()을 완전히 오버라이드함.
• image_embeddings와 vae latent를 분리해서 encode 후,
• 반복적인 gradient optimization 루프를 사용함 (latents.requires_grad_()).
• denoising step에서 각 tile별 loss를 계산하고 gradient 업데이트 수행.
⚙️ Diffusers 구성 요소
구성 요소설명
| vae | AutoencoderKLTemporalDecoder – 이미지에서 latent space로 인코딩/디코딩 |
| image_encoder | CLIP-ViT-H-14 image encoder – 이미지를 임베딩 |
| unet | UNetSpatioTemporalConditionModel – latent denoising |
| scheduler | EulerDiscreteScheduler – timestep별 latent 업데이트 |
| image_processor | VAE에 적합하게 이미지 전처리 수행 |
📦 Output
• frames: 렌더링된 프레임들 (25장)
• generated.mp4: 25프레임을 FPS=7로 변환한 비디오 파일
🎯 차별점 및 주요 특성
1. Stable Video Diffusion을 NVS task에 맞게 커스터마이징
2. Depth 기반 forward warping을 통해 cond image 생성
3. Tile-wise optimization을 통해 학습 없는 test-time optimization 적용
4. lambda_ts를 동적으로 추정하여 frame별 weight 조절
• mask와 cond image의 역할이 중요 — inpainting + 조건 프레임 정보 제공
• lambda_ts는 frame마다 달라지며, 학습된 모델과 유기적으로 결합됨
좋아요, 질문 하나하나 아주 구체적으로 설명해줄게. NVS-Solver를 처음 접한 상태라고 생각하고, 개념부터 맥락까지 연결해서 풀어줄게.
1. search_hypers() 함수에서 생성하는 lambda_ts는 무슨 역할?
• lambda_ts는 각 프레임(timestep)마다 얼마나 optimization loss를 반영할지를 결정하는 weight 값 리스트야.
• NVS-Solver는 렌더링 도중 test-time optimization을 하는데, lambda_t가 크면 해당 프레임에서 더 많은 최적화를 하게 돼. 반대로 작으면 거의 건드리지 않아.
• 즉, lambda_ts는 “이 프레임은 중요한 장면이니까 더 최적화하고, 이 프레임은 거의 고정 이미지처럼 써도 돼”라는 프레임별 importance 조절 장치야.
lambda_ts는 각 프레임마다 적용되는 loss weight 조절값이에요.
• svd_render() 안에서 iterative하게 latent를 업데이트할 때, 학습은 하지 않지만, 마치 학습하듯이 test-time optimization을 해요.
• 이때 각 프레임에 대해 얼마나 강하게 loss를 반영할지 조절하는 계수가 바로 lambda_t.
• 즉, 어떤 프레임은 좀 더 정확하게 맞춰주고, 어떤 프레임은 덜 민감하게 다뤄요.
👉 예: 초반 프레임에는 예측이 잘 되니까 weight 낮게, 나중 프레임에는 예측 어려우니까 weight 높게. 그걸 lambda_ts 리스트로 frame별로 갖고 있음.
2. sigma는 왜 쓰이는 건가?
• sigma는 optical flow 기반 warping 오차량 또는 각 프레임의 불확실성을 나타내는 값이야.
• warping으로 만든 frame이 원래 프레임과 얼마나 달라졌는지, 즉 “이 프레임은 덜 정확하다”는 신호를 주는 거지.
• sigma가 높을수록 해당 프레임은 더 불안정한 조건에서 생성되었으니, 더 최적화해야 한다고 판단해.
• 그래서 search_hypers()는 sigma를 기준으로 lambda_ts weight를 조절해주는 거야.
각 프레임에 대한 난이도 또는 difficulty를 나타내는 값으로 활용돼요.
• 보통 시그마는 영상 흐름에서 변화량 또는 모션 정도, 혹은 warp 시 불확실도를 의미하는 척도예요.
• 이 sigma 값들을 기반으로 lambda_ts를 계산해요.
• sigma가 크면 → 불확실함이 크다 → 해당 프레임을 더 정교하게 다뤄야 하니까 lambda↑
즉, sigma → 어려운 프레임 식별 → lambda_ts 조절 로 이어지는 구조예요.
3. 각각의 모듈 설명 (vae, unet 등)
모듈 이름역할
| vae: AutoencoderKLTemporalDecoder | 이미지/비디오를 압축된 latent로 encode하고, 다시 원래 이미지로 decode해주는 역할. 이 프로젝트에서는 프레임 단위가 아니라 시간축도 고려한 temporal decoder 사용. |
| image_encoder: CLIP-ViT-H-14 | - 원본 이미지를 CLIP 모델로 인코딩해서 고차원 image embedding을 생성- 이 embedding은 UNet이 “이 이미지 기반으로 비디오 만들어야지”라고 인식하는 단서 CLIP의 Vision Transformer. 입력 이미지의 의미/특징을 추출해서, 조건(condition)으로 사용. 영상 생성 시 “이런 의미의 장면이 되어야 해”라고 가이드를 줌. |
| unet: UNetSpatioTemporalConditionModel | - diffusion 과정에서 latent를 noise 제거하며 점점 복원해나가는 핵심 네트워크- 시간과 공간 정보를 함께 고려하는 구조 VAE latent 공간에서 노이즈를 제거해주는 핵심 모델. 시간축 정보(SpatioTemporal)까지 반영해서 여러 프레임을 동시에 고려하며 denoising. |
| scheduler: EulerDiscreteScheduler | - diffusion step에서 latent에 noise를 얼마나 추가할지 / 제거할지를 조절하는 장치- scale_model_input() 같은 함수는 timestep에 따라 noise level을 조정해줘 |
| image_processor: VaeImageProcessor | - 이미지를 latent로 encode하거나, latent를 이미지로 decode할 때 이미지 전처리 후처리를 해주는 helper 모듈 |
4. “25프레임을 FPS=7로 변환”이 무슨 뜻?
• 말 그대로, 생성된 25장의 비디오 프레임을 초당 7장씩 재생되는 비디오로 만든다는 뜻이야.
• 즉, 생성된 이미지를 비디오로 저장할 때 프레임 간 간격을 결정하는 숫자가 fps = 7.
• 그러면 전체 영상 길이는: 25 frames / 7 fps ≈ 3.57초
5. “lambda_ts를 동적으로 추정하여 frame별 weight 조절”이 무슨 의미?
• lambda_ts는 각 프레임의 warping 오차(sigma)를 기반으로 자동 계산됨.
• 즉, “이 프레임은 왜곡이 심하니 더 최적화하자”, “이 프레임은 거의 문제 없으니 그대로 두자” 같은 전략을 자동으로 세움.
• 이는 모든 프레임에 동일한 loss를 주는 것보다, 전체 시퀀스 품질 향상에 효과적이야.
6. cond image가 뭐야?
• condition image의 줄임말. 말 그대로 조건 이미지야.
• 원본 이미지 하나로 25프레임 비디오를 만들려면, 중간 프레임들을 예측해야 함.
• 이때 camera를 회전시키며 만든 여러 뷰(→ forward warping 이미지들)를 cond image로 사용함.
• 이 조건 이미지를 보고 “이렇게 회전하면 이런 이미지가 나와야겠군”이라고 학습된 모델이 프레임을 생성하는 데 도움을 받는 거야.
7. forward warping vs. 일반 warping
개념설명
| 일반 warping (backward warping) | - target 위치의 값을 source image에서 sampling하는 방식- 대부분의 warping은 이 방식을 사용 |
| forward warping | - source image의 각 픽셀을 target image로 보내는 방식- 하지만 target pixel이 비게 될 수 있어 → hole 발생 가능- bilinear splatting 같은 보간법으로 해결 |
| 차이점 핵심 | - forward warping은 렌더링/투영 방식과 유사해서 카메라 회전 시뮬레이션에 적합함- backward는 상대적으로 매끄럽지만 기하학적으로 직관적이지 않음 |
8. “Tile-wise optimization을 통해 학습 없는 test-time optimization 적용”이란?
• “학습 없는”이란 말은, 사전 학습된 모델을 다시 fine-tune하지 않고, 단지 테스트 중에 최적화를 한다는 뜻이야.
• 근데 한 번에 전체 이미지(latent)를 최적화하면 GPU 메모리가 너무 커져.
• 그래서 이미지를 4등분(또는 타일 tile 단위로)으로 나눠서 각 부분만 순차적으로 최적화함.
• 이걸 tile-wise optimization이라고 해.
즉, 학습 없이도 각 프레임에 대해서만 부분적으로 latent를 최적화해서 품질을 끌어올리는 방식!
필요하면 각 모듈별 그림이랑 동작 흐름도 만들어줄게. 이거 읽고 이해 안 가는 부분 있으면 바로 질문 줘.
코드에서 이미지 리사이즈(Resize)는 어디서 일어나는가?
🔍 리사이즈 발생 위치
1) save_warped_image() 함수 안에서
image_o = PIL.Image.open(image_path)
image_o = image_o.resize((1024,576),PIL.Image.Resampling.NEAREST) # ✅ 여기• 이 줄에서 입력 이미지를 무조건 (1024, 576) 사이즈로 강제로 리사이즈하고 있어요.
• 그 후에 depth도 같은 크기로 리사이즈되므로, 이 크기가 전체 파이프라인의 기준 해상도가 됩니다.
2) _resize_with_antialiasing() 함수 안에서
• 이건 StableVideoDiffusionPipeline 클래스 내 _encode_image() 함수에서 호출됩니다:
image = _resize_with_antialiasing(image, (224, 224))• 이건 CLIP image encoder에 들어가기 위한 리사이즈예요.
• 여기서 잠깐 224로 줄였다가 다시 feature로 쓰이기 때문에 최종 출력 이미지 해상도에는 영향 안 줍니다.
• 이건 VIT의 입력 조건을 맞추기 위한 필수 리사이즈예요.
리사이즈 안 하고 원본 해상도 유지하려면?
1. image_o.resize((1024,576)) ➡️ 주석 처리하거나 삭제
2. 대신 원본 크기를 유지하려면, 아래처럼 처리해야 합니다:
original_width, original_height = image_o.size그리고 모든 downstream 코드에서 이 original_width, original_height를 쓰도록 수정해야 해요 (예: cv2.resize(depth, (w, h))).
✅ 하지만 문제는: diffusion pipeline 내부에서는 UNet 및 VAE가 8의 배수 크기를 기대합니다. 즉, 크기가 8의 배수가 아니면 에러가 나거나 성능이 떨어질 수 있어요.
• 그러니 최소한 8의 배수로 크기만 맞춰주는 수준의 리사이즈는 필요해요.
한 장 처리에 8분 40초 걸림. 시간 줄이려면?
🚀 개선 포인트 요약
항목시간 줄어듬설명
| ✅ export_to_video() 제거 | ✅ 매우 큼 | .mp4로 저장하는 데 시간이 꽤 걸림. |
| ✅ 이미지 저장 최소화 | ✅ | PNG 여러 장 저장도 느림. 특정 프레임만 저장하도록 변경 가능 |
📌 export_to_video() 제거 방법
svd_render() 함수 마지막 부분에서:
export_to_video(frames, os.path.join(output_path,"generated.mp4"), fps=7)이 줄을 주석 처리하거나 삭제하세요.
또는 특정 시점 프레임만 저장하고 싶다면:
# 전체 프레임 저장 (기존)
for i,fr in enumerate(frames):
fr.save(os.path.join(output_path, f"{i:06d}.png"))
# 특정 프레임만 저장 (예: 중간 프레임)
frames[12].save(os.path.join(output_path, f"{12:06d}.png"))
⏱ 예시: 빠르게 돌릴 설정
--num_inference_steps 25 \
--decode_chunk_size 25 \또는 코드 안에서 default 값을 다음처럼 바꿔도 됨:
num_inference_steps=25
decode_chunk_size=25
✅ 정리
항목액션
| ❌ image.resize((1024,576)) | 주석 처리하고 원본 크기 사용 |
| ⛔ 단, 8의 배수는 맞춰야 함 | (576, 1024) → (576, 1024)처럼 유지 |
| ✅ export_to_video() 제거 | 속도 확 줄어듦 |
| ✅ inference step 수 줄이기 | 예: 25 or 50 |
| ✅ 특정 프레임만 저장 | frames[i] 선택 저장 |
✅ 1. VAE latent 공간이 뭐야?
🔹 VAE란?
• VAE는 Variational Autoencoder의 약자예요.
• 이미지를 낮은 차원의 “잠재 공간(latent space)“에 압축한 후, 다시 복원하는 구조입니다.
🔹 Latent 공간이란?
• 이미지 전체를 작고 압축된 벡터로 표현한 공간이에요.
• 예: 원래 이미지가 3x576x1024라면, VAE의 latent는 4x72x128처럼 작음 (약 8배 축소)
• 이 latent를 가지고 denoising을 하거나, 시간적으로 변화하는 latent를 만들어서 영상 생성에 사용합니다.
✅ 2. 여러 프레임을 어떻게 동시에 고려해?
🔹 UNetSpatioTemporalConditionModel
• UNet은 기본적으로 **하나의 이미지(또는 latent)**를 처리합니다.
• 근데 SpatioTemporal UNet은 **시간축(t)**이 포함된 입력을 처리할 수 있어요.
예시:
• latent: [B, F, C, H, W] → 여기서 F는 frame 수
• 즉, 25개의 프레임 latent를 한 번에 받아들여서, 시간적으로 연속성을 유지하면서 처리해요.
💡 왜 필요한가?
• 일반 diffusion 모델은 이미지 하나만 보고 noise 제거함
• Video diffusion은 프레임이 이어져야 자연스러움 → 그래서 “동시에 고려”함
✅ 3. Splatting이 뭐야?
🔹 Splatting은 “forward warping”과 관련된 기술입니다.
• 픽셀을 “쏜다(splat)“는 개념 → 3D 공간에서 다음 프레임 위치로 픽셀을 날려서 영상 생성
🔹 이 프로젝트에서는 bilinear splatting 사용
• depth와 camera pose를 이용해서 1번 프레임의 픽셀들을 다음 프레임 위치로 forward warp 함
• 단순 이동이 아니라 subpixel 위치로 부드럽게 보간(bilinear interpolation) 해주는 게 splatting의 핵심
✅ 4. 스케줄링(scheduling)이란?
🔹 Diffusion 모델의 핵심 개념
• 학습은 이미지에 점점 noise를 추가하는 과정
• 샘플링은 노이즈를 점점 줄여나가는 과정
🔹 스케줄러 역할
• 몇 step에 어떤 정도의 noise를 써야 할지를 정해줍니다
• EulerDiscreteScheduler는 한 스텝씩 점진적으로 denoise할 때 noise 크기 조절, scale 조절을 해줘요
✅ 5. lambda는 뭐야?
🔹 의미
• lambda_t는 각 프레임마다 얼마나 “조건 영상(cond image)“을 강하게 따라가야 하는지를 정하는 weight예요.
• 쉽게 말하면:
프레임 번호lambda_t 값해석
| 0 | 1.0 | cond image를 강하게 따라가라 |
| 24 | 0.1 | 거의 안 따라가도 됨 |
🔹 왜 중요해?
• 시간 흐름에 따라 점점 자유롭게 생성하게 만들기 위해 조절함
✅ 6. 쉬운 프레임은 덜 수정한다는 게 무슨 뜻이야?
🔹 “쉬운 프레임”이란?
• 초기 프레임에 가까운 영상은 **condition image (warped image)**로부터 매우 비슷해요.
• 즉, 이미 충분히 잘 warp 되었기 때문에 많이 손대지 않아도 괜찮은 프레임
🔹 반면, 뒤로 갈수록?
• 예측된 warp가 점점 어려워짐
• motion이 커지고 depth 오류 누적 → 더 많은 보정 필요 → lambda를 작게 잡고 학습된 priors에 더 의존
✅ 7. cond image가 뭐야?
🔹 Condition image (cond image)
• “조건 영상”이에요.
• 예를 들어, 1번 이미지에서 2번 카메라 뷰로 depth+pose 기반 warp 한 영상이 cond image
• UNet은 이 cond image를 참고해서 더 자연스럽게 보정된 프레임을 생성합니다.
✅ 8. Forward warping vs 일반 warping
방식의미
| Forward warping (splatting) | 원본의 각 픽셀을 다음 위치로 보내는 방식 |
| Backward warping | 다음 위치에서 원래 위치를 참조해서 가져오는 방식 |
• Forward warping은 occlusion, disocclusion을 더 잘 다룰 수 있음
• 이 프로젝트에서는 forward warping → inpainting → denoise 방식
✅ 9. Tile-wise optimization을 통해 학습 없는 test-time optimization
🔹 무슨 말이야?
• 기존엔 모델을 학습(training)해서 써야 했음
• 여기선 이미 학습된 모델을 고정한 채, 테스트 시점(test-time)에 입력을 최적화함
🔹 Tile-wise란?
• 전체 프레임을 4개의 타일로 나누고, 각각에 대해 loss를 계산하고 backpropagation 함
프레임영역처리 방식
| 전체 | 좌상단, 우상단, 좌하단, 우하단 | 각각 grad 계산해서 병합 |
• GPU 메모리 절약 + 더 세밀한 local 보정 가능
📌 정리하면:
개념설명
| latent 공간 | 압축된 이미지 표현 공간 |
| spatiotemporal UNet | 여러 프레임을 시간적으로 함께 보고 denoise |
| splatting | depth+pose로 forward warp하는 보간 방식 |
| scheduler | 노이즈 제거 강도 조절 |
| lambda_t | 프레임마다 condition 따라가는 강도 |
| 쉬운 프레임 | condition image와 유사한, 덜 수정해도 되는 프레임 |
| cond image | depth+pose로 warp한 영상 |
| test-time optimization | 학습 없이 test 시점에만 local gradient descent로 보정 |
| tile-wise | 메모리 줄이기 위해 영역별로 최적화 수행 |