[이론] Lloyd-Max Quantizer 자세한 수식 유도 설명

먼저 흐름을 파악하려면 이 글들을 참고하는 것이 좋다.

https://minsunstudio.tistory.com/103

[CV] Image degradation 직접 구현 -① (Blur, Periodic Noise, Low Contrast)

 

https://minsunstudio.tistory.com/104

[CV] Image Processing 개념 총정리! / Image degradation 직접 구현 -②③ (Blur, Periodic Noise, Low Contrast)

 

https://minsunstudio.tistory.com/105

[CV] FFT란 Fast Fourier Transform

 

---

Image Quantization (영상 양자화)

정의

• 연속 밝기 값을 유한한 레벨로 변환하는 과정.
  • 예: 256단계(8bit), 4096단계(12bit) 등.
• 영상 센서가 빛의 세기를 전압으로 변환하고, 이를 디지털 수로 표현.
  • Dynamic range = 전압이 표현할 수 있는 범위.

비트 깊이

• 4 level (2bit): 밴딩(banding) 현상 심함.
• 8bit (256 gray levels): 일반 영상 표준.
• 12bit 이상: 의료 영상(DICOM, NIfTI)에서 필수 — 진단 정확도 향상.

Quantizer 종류

1. Uniform Quantizer : 등간격 양자화.
2. Lloyd–Max Quantizer : MSE (평균제곱오차)를 최소화하도록 적응형 양자화.
   • uuu: 원본 신호, u′u'u′: 양자화 결과.
   • 반복적으로 오차 계산 → 수렴할 때까지 갱신.
3. Vector Quantization : 픽셀 단독이 아닌 인접 픽셀 벡터를 한꺼번에 양자화하여 공간 상관성 활용.

 

수식 유도 자세한 설명

 

---

 개념 정리: Quantization(양자화)란?

연속적인 입력 신호(continuous value)를 한정된 개수의 이산 값(discrete value)으로 변환하는 과정.

• 영상에서는 픽셀의 밝기값(intensity) 이 0~255 같은 정수로 표현되죠?
• 실제 센서로 받은 값은 연속적인 전압(예: 0~1V) 형태예요.
  → 이를 디지털로 저장하려면 이산화(quantization) 해야 합니다.

즉,
아날로그(continuous) → 디지털(discrete) 로 바꾸는 핵심 단계예요.

---

GOAL

Continuous (또는 Discrete) 값을 Discrete 값으로 변환
→ 결과적으로 데이터 압축(Compression) 또는 디지털화 달성.

---

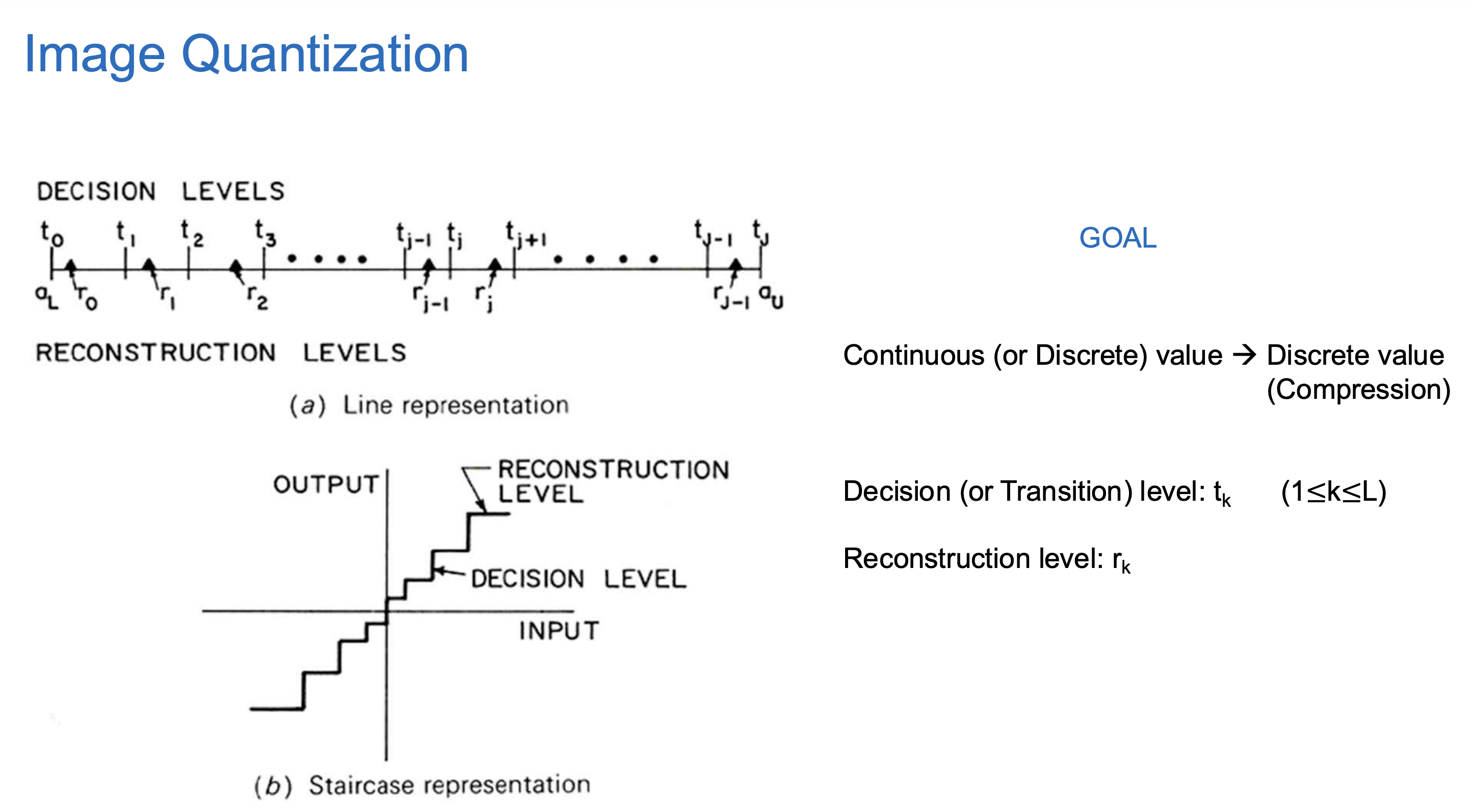
주요 구성 요소

양자화기는 두 가지 레벨을 정의합니다:

이름 기호 의미

Decision level	( t_k )	구간의 경계값 (어디까지 같은 값으로 취급할지 결정)
Reconstruction level	( r_k )	구간 내부 값을 대표하는 값 (실제 출력되는 양자화 값)

---

(1) Line representation (위 그래프)

• 입력 값 축이 (u_L) ~ (u_U) 범위를 갖고 있음 (연속)
• 이 범위를 여러 interval 로 나눔
  → ( [t_{k-1}, t_k] ) 구간
• 각 구간을 대표하는 reconstruction level (r_k) 로 표현

즉,

“입력이 어느 구간에 속하느냐에 따라 일정한 대표값으로 대체”

---

(2) Staircase representation (아래 그래프)

이건 실제 입력-출력 관계를 시각화한 것입니다.

• x축: 입력 (continuous)
• y축: 출력 (quantized, discrete)
• 결과적으로 계단(staircase) 형태의 그래프가 됩니다.

즉,
입력이 조금 달라도 같은 구간이면 같은 출력이 나옵니다.
→ 정보 손실(lossy) 발생
→ 그러나 데이터 표현은 단순해짐 (압축 효과)

---

두 번째 슬라이드 — Lloyd-Max Quantizer (로이드-맥스 양자화기)

이제 “어떻게 하면 가장 효율적으로 양자화하느냐”를 수학적으로 풀어내는 단계예요.
즉, Mean Squared Error (MSE) 를 최소화하는 최적의 (t_k, r_k) 값을 찾는 게 목표입니다.

 

목적

MSE를 최소화하는 ( t_k, r_k )를 찾자.
(→ 최적의 quantizer 설계 문제)

이를 Lloyd-Max quantizer라고 부릅니다.

 

Lloyd–Max Quantizer 도출 과정

Lloyd와 Max가 제시한 수학적 조건은 다음 두 가지예요.

---

(1) Reconstruction level ( r_k ) (대표값) 선택

구간 내부에서 오차가 최소가 되려면,
[
r_k = \frac{\int_{t_{k-1}}^{t_k} u P_u(u) du}{\int_{t_{k-1}}^{t_k} P_u(u) du} = E[u \mid u \in T_k]
]

즉,
해당 구간 (T_k) 안에서의 기댓값(평균) 으로 선택해야 합니다.

→ 구간 내 확률분포가 균일하면 단순히 중간값(mean) 이 됩니다.

---

(2) Decision level ( t_k ) (경계값) 선택

두 구간의 경계에서는
양자화된 두 값 사이의 오차가 같아야 합니다.

즉,
[
t_k = \frac{r_k + r_{k+1}}{2}
]

→ 두 reconstruction level의 중간 지점이 경계가 됩니다.

---

(3) Lloyd–Max 알고리즘의 절차 요약

1️⃣ 초기값으로 (t_k, r_k) 설정
2️⃣ (t_k) 고정 후 → (r_k) 계산 (평균값)
3️⃣ (r_k) 고정 후 → (t_k) 갱신 (중간값)
4️⃣ 수렴할 때까지 반복

이게 바로 Lloyd algorithm (k-means와 유사한 iterative quantization) 의 핵심이에요.

---

그래프 해석

그래프 의미

위 (Line representation)	구간과 대표값의 선형적 대응 관계
아래 (Staircase representation)	실제 입력–출력 관계 (계단형)

→ 입력 신호가 변화해도 출력은 “계단 단위로” 바뀌며,
그 계단의 높이(출력값)가 (r_k), 경계가 (t_k) 입니다.

 

입력 신호 (continuous)	(u)	원래의 연속 값
출력 신호 (quantized)	(u')	양자화 후 재구성된 값
Decision level	(t_k)	경계 값, 어느 구간에 속하는지 결정
Reconstruction level	(r_k)	구간 대표값, 출력되는 양자화 값
목표	(\min E[(u-u')^2])	MSE 최소화
조건식	(r_k = E[u	u \in T_k],\ t_k = \frac{r_k + r_{k+1}}{2})

 

Quantization	연속 값을 이산 값으로 바꾸는 과정 (디지털화, 압축)
결과 형태	계단형(staircase) 출력
문제점	오차 발생 (MSE)
해결책	Lloyd–Max Quantizer로 MSE 최소화
핵심 아이디어	각 구간의 평균값을 대표값으로, 인접 대표값의 중간을 경계로 설정
결과	최소 오차 기반의 최적 양자화기 (image, audio, compression 등에서 사용)